Cho tứ diện ABCD có AB = AC = AD = 24, BC = CD = DB = 15. Trên cạnh AB lấy
Câu hỏi:
Cho tứ diện ABCD có AB = AC = AD = 24, BC = CD = DB = 15. Trên cạnh AB lấy điểm P sao cho PA = x.PB. Với giá trị nào của x thì mặt phẳng (a) qua P song song với AC và BD cắt tứ diện ABCD theo thiết diện là một hình thoi?
Trả lời:
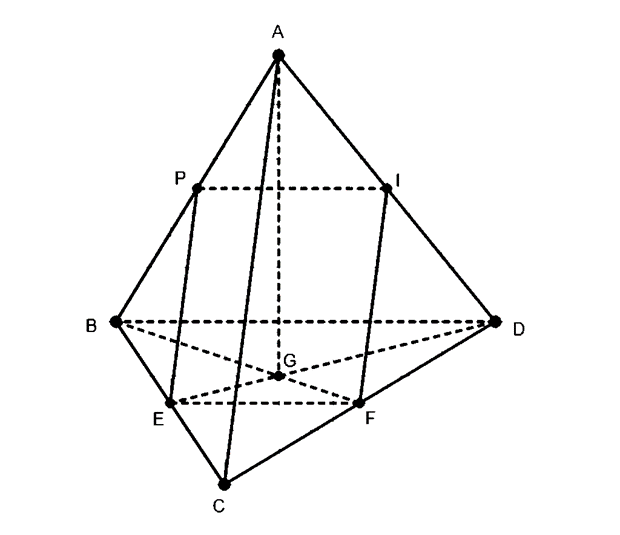
PA = x.PB suy ra: \(\frac{{PA}}{{PB}} = x\)
⇒ \(\frac{{PA}}{{PB + PA}} = \frac{x}{{1 + x}}\)
⇒ \(\frac{{PA}}{{AB}} = \frac{x}{{1 + x}}\) và \(\frac{{PB}}{{AB}} = \frac{1}{{1 + x}}\)
Tam giác BAD dựng PI // BD ⇒ \(\frac{{PI}}{{BD}} = \frac{{AP}}{{AB}}\)
Tam giác BAC dựng PE // AC ⇒ \(\frac{{PE}}{{AC}} = \frac{{BP}}{{BA}}\)
(PIE) chính là (α), dựng IF // AC
⇒ PIFE là thiết diện của hình chóp (ABCD) cắt bởi (α)
Do IF//PE và IF = PE nên PIFE là hình bình hành để tứ giác là hình thoi thì PI = PE
Mà \(PI = \frac{{AP}}{{AB}}.BD = \frac{x}{{x + 1}}.15\)
\(PE = \frac{{BP}}{{BA}}.AC = \frac{1}{{x + 1}}.24\)
PI = PE ⇒ 15x = 24 ⇒ x = \(\frac{{24}}{{15}}\).

