Câu hỏi:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, biết AB = AC = AD = 1. Số đo góc giữa hai đường thẳng AB và CD bằng?
Trả lời:
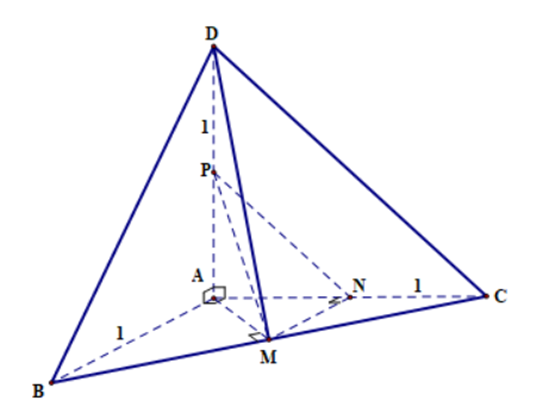
Vì AB ⊥ AC (giả thiết) và AB ⊥ AD (giả thiết)
Mà AC ∩ AD = {A}; AC, AD cùng thuộc mặt phẳng (ACD)
Suy ra: AB ⊥ (ADC)
Suy ra: AB ⊥ CD
Nên \(\widehat {\left( {AB;CD} \right)} = 90^\circ \).
Câu 1:
Trong mặt phẳng cho 15 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Số tam giác có đỉnh là 3 trong số 15 điểm đã cho là?
Câu 3:
Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.
Câu 4:
Làm theo mẫu: \(\frac{{143}}{{10}} = 14;\frac{3}{{10}} = 0,3\).
Yêu cầu: \(\frac{{126}}{{100}} = ...;\frac{{26}}{{100}} = ...\)
\(\frac{{1246}}{{10}} = ...;\frac{6}{{10}} = ...\)
Câu 5:
Có bao nhiêu cách sắp ngẫu nhiên 10 học sinh gồm 2 học sinh 11A, 3 học sinh lớp 11B và 5 học sinh lớp 11C thành 1 hàng ngang sao cho không có học sinh nào cùng lớp đứng cạnh?
Câu 7:
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
