Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi M là trung điểm của AB
Câu hỏi:
Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi M là trung điểm của AB. Mp(P) qua M và song song với BC và CD cắt tứ diện theo 1 thiết diện là
A. Một tam giác cân;
B. Một tam giác đều;
C. Một hình bình hành;
D. Một tứ giác.
Trả lời:
Đáp án đúng là: B
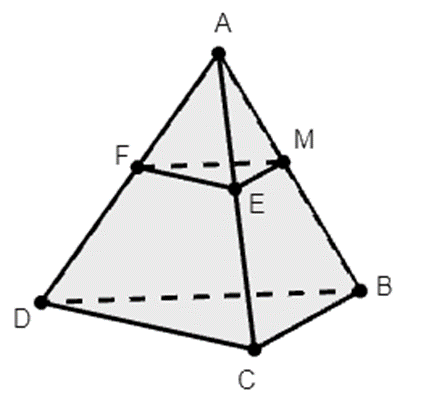
Gọi E và F lần lượt là trung điểm của AC và AD ta có ME // BC, EF // CD
\(\left\{ \begin{array}{l}M \in \left( P \right) \cap \left( {ABC} \right)\\\left( P \right)//BC \subset \left( {ABC} \right) \Rightarrow \left( P \right) \cap \left( {ABC} \right) = ME\\ME//BC\end{array} \right.\)
\(\left\{ \begin{array}{l}E \in \left( P \right) \subset \left( {ACD} \right)\\\left( P \right)//CD \subset \left( {ACD} \right) \Rightarrow \left( P \right) \cap \left( {ACD} \right) = EF\\EF//CD\end{array} \right.\)
(P) ∩ (ABD) = MF.
Khi đó thiết diện tạo bởi mp(P) và hình chóp là tam giác MEF
Ta có: \(ME = \frac{1}{2}BC = \frac{1}{2}a\); \(EF = \frac{1}{2}CD = \frac{1}{2}a\);
\(MF = \frac{1}{2}BD = \frac{1}{2}a\)
\( \Rightarrow ME = EF = MF = \frac{a}{2}\).
Vậy thiết diện là một tam giác đều.