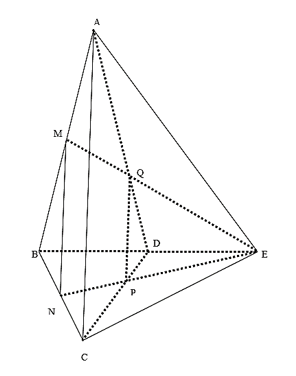
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, tron

Khẳng định nào sau đây sai?

Câu nào trong các câu sau không phải là mệnh đề?

Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng $\widehat{SBC}=\widehat{SCD}=90°$.

Cho hình nón N₁ có chiều cao bằng 40 cm. Người ta cắt hình nón N₁ bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N₂ có thể tích bằng 18 thể tích N₁. Tính chiều cao của hình nón N₂.

Cho hàm số y = f(x) có đạo hàm f'(x) = x²(x − 1)(x + 2)²(x − 2). Tìm số điểm cực trị của hàm số đã cho.

Vẽ đồ thị hàm số y = x².

Vẽ đồ thị các hàm số y = –x ² và y = x – 2 trên cùng một hệ trục tọa độ.