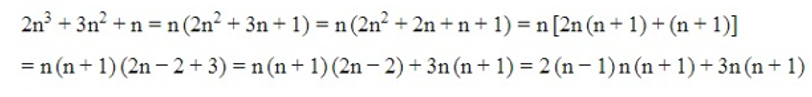Chứng minh 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Câu hỏi:
Chứng minh 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Trả lời:
Ta có:
Ta thấy (n – 1), n, (n + 1) là 3 số nguyên liên tiếp
Suy ra (n – 1)n(n + 1) chia hết cho 2 và 3
Do đó 2(n – 1)n(n + 1) ⋮ 6
Có n(n + 1) ⋮ 2
Suy ra 3n(n + 1) ⋮ 6
Do đó 2(n – 1)n(n + 1) + 3n(n + 1) ⋮ 6
Vậy 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Có bao nhiêu số tự nhiên chẵn có 4 chữ số chia hết cho 9?
Xem lời giải »
Câu 3:
Một tháng có ba ngày chủ nhật đều là ngày chẵn. Ngày 15 tháng đó là thứ mấy?
Xem lời giải »
Câu 4:
Một người mua một số cam, sau khi bán hết người đó thu được 682 500 đồng. Tính ra người đó lãi được 18% giá bán. Hỏi giá vốn số cam đó là bao nhiêu?
Xem lời giải »
Câu 5:
Tìm các cặp số tự nhiên x, y biết: 6xy – 9x – 4y + 5 = 0.
Xem lời giải »
Câu 6:
Cho tam giác ABC. Trên tia đối của AB lấy D sao cho AD = AC, trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh 3 điểm M, A, N thẳng hàng.
Xem lời giải »
Câu 7:
Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AB, trên tia đối của tia AC lấy điểm E sao cho AE = AC
a) Chứng minh rằng: BE = CD.
Xem lời giải »