Chứng minh n4 + 64 là hợp số với mọi n ∈ ℤ.
Câu hỏi:
Trả lời:
n4 + 64 = (n2 + 8)2 – (4n)2 = (n2 + 8 – 4n)(n2 + 8 + 4n)
Ta thấy: n4 + 64 chia hết cho n2 + 8 – 4n và n2 + 8 + 4n tức n4 + 64 có nhiều hơn 2 ước.
Vậy n4 + 64 là hợp số.
Câu hỏi:
Trả lời:
n4 + 64 = (n2 + 8)2 – (4n)2 = (n2 + 8 – 4n)(n2 + 8 + 4n)
Ta thấy: n4 + 64 chia hết cho n2 + 8 – 4n và n2 + 8 + 4n tức n4 + 64 có nhiều hơn 2 ước.
Vậy n4 + 64 là hợp số.
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
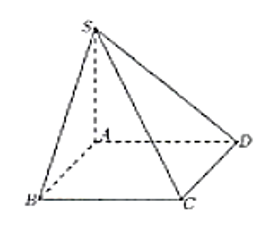
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Câu 6:
. Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) A = {0; 3; 6; 9; 12; 15};
b) B = {5; 10; 15; 20; 25; 30};
Câu 7:
Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
d) D = {1; 5; 9; 13; 17}.
Câu 8:
