Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = y – x trên miền xác định bởi hệ
Câu hỏi:
Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = y – x trên miền xác định bởi hệ \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\]
A. Fmin = 1.
B. Fmin = 2.
C. Fmin = 3.
D. Fmin = 4.
Trả lời:
Đáp án đúng là: A
\[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y - 2x - 2 \le 0\\2y - x - 4 \ge 0\\x + y - 5 \le 0\end{array} \right.\] (*)
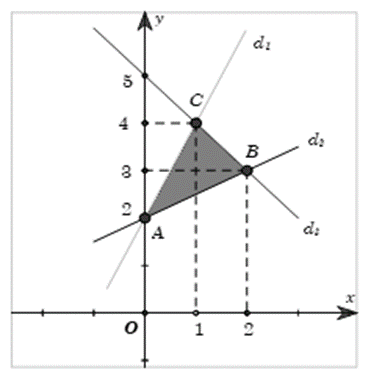
Trong mặt phẳng tọa độ Oxy vẽ các đường thẳng d1:y − 2x − 2=0, d2: 2y − x− 4= 0, d3: x + y − 5 = 0.
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng (tam giác ABC kể cả biên) tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ (*) là
A(0; 2), B(2; 3), C(1; 4).
Ta có: \[\left\{ \begin{array}{l}F\left( {0;2} \right) = 2\\F\left( {2;3} \right) = 1\\F\left( {1;4} \right) = 3\end{array} \right.\]
Suy ra Fmin = 1.

