Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. a) Tính diện
Câu hỏi:
Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông.
a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.
b) Tính thể tích của khối nón.
Trả lời:
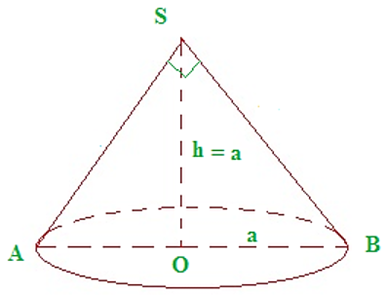
Thiết diện qua trục là tam giác vuông SAB có \(\widehat {ASB} = 90^\circ \), mà SA = SB nên suy ra tam giác ASB vuông cân tại S. Suy ra \(\widehat {SBO} = 45^\circ \Rightarrow OB = OS = a\) hay R = a.
Vì tam giác SOB vuông nên độ dài đường sinh là:
\(l = SB = \sqrt {S{O^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Diện tích xung quanh của hình nón là:
\({S_{sq}} = \pi \,.\,a\,.\,a\sqrt 2 = \pi {a^2}\sqrt 2 \) (đvdt)
Diện tích toàn phần của hình nón là:
\({S_{tp}} = {S_{xq}} + {S_{d\'a y}} = \pi \,.\,a\,.\,a\sqrt 2 + \pi \,.\,{a^2} = \left( {\sqrt 2 + 1} \right)\pi {a^2}\) (đvdt)
Thể tích của khối nón là:
\(V = \frac{1}{3}\pi {R^2}\,.\,h = \frac{1}{3}\pi \,.\,{a^2}\,.\,a = \frac{1}{3}\pi {a^3}\) (đvdt)

