Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg ch

Lời giải

Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.

Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\end{array} \right.\).

Theo đề, ta có từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B.

⇒ Từ x tấn nguyên liệu loại I, có thể chiết xuất được 20x kg chất A và 0,6x kg chất B.

Theo đề, ta có từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B.

⇒ Từ y tấn nguyên liệu loại II, có thể chiết xuất được 10y kg chất A và 1,5y kg chất B.

Như vậy ta chiết xuất được 20x + 10y (kg) chất A và 0,6x + 1,5y (kg) chất B.

Khi đó ta có hệ điều kiện là:

\(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\20x + 10y \ge 140\\0,6x + 1,5y \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\,\,\,\,\,\left( * \right)\)

Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 4x + 3y đạt giá trị nhỏ nhất.

Vẽ và xác định miền nghiệm của (*):

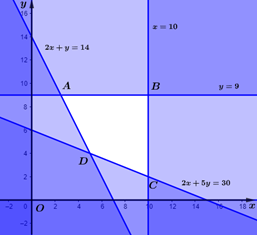
Ta có:

⦁ Miền nghiệm của (*) là tứ giác ABCD (kể cả biên).

⦁ \(A\left( {\frac{5}{2};9} \right),\,B\left( {10;9} \right),\,C\left( {10;2} \right),\,D\left( {5;4} \right)\).

⦁ F(A) = 37, F(B) = 67, F(C) = 46, F(D) = 32.

Suy ra minF(x; y) = F(D) = 32 khi và chỉ khi x = 5, y = 4.

Vậy để chi phí mua nguyên liệu là ít nhất thì cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.