Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng B qua C. Độ dài đoạn AD
Câu hỏi:
Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng B qua C. Độ dài đoạn AD.
Trả lời:
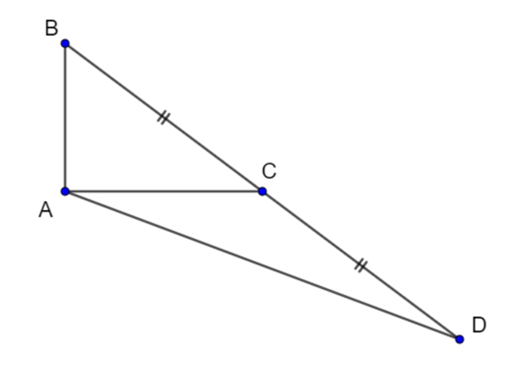
a = 5; b = 4; c = 3 ⇒ BC = 5; AC = 4; AB = 3
D đối xứng với B qua C ⇒ C là trung điểm của BD
⇒ \(BC = \frac{1}{2}BD \Rightarrow BD = 2BC = 2.5 = 10\)
Xét tam giác ADB có AC là đường trung tuyến
⇒ \(A{C^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\)
⇔ \({4^2} = \frac{{2\left( {{3^2} + A{D^2}} \right) - {{10}^2}}}{4}\)
⇔ 18 + 2AD2 – 100 = 64
⇔ AD2 = 73
⇔ \(AD = \sqrt {73} \).

