Tam giác ABC. Gọi D, E, F lần lượt là trung điểm của cạnh AB, AC, BC và M, N, P, Q theo thức tự là trung

Tam giác ABC. Gọi D, E, F lần lượt là trung điểm của cạnh AB, AC, BC và M, N, P, Q theo thức tự là trung điểm của đoạn thẳng DA, AE, EF, FD

a. Chứng minh: EF là đường trung bình của tam giác ABC.

b. Chứng minh: Tứ giác DAEF, MNPQ là hình bình hành.

c. Khi tam giác ABC vuông tại A thì các tứ giác DAEF, MNPQ là hình gì?

d. Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông

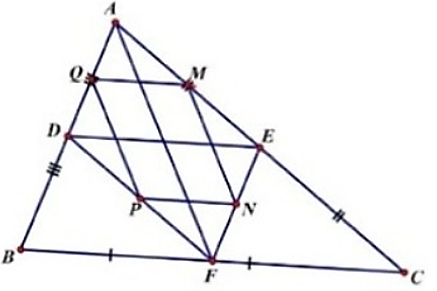
a) ΔABC có:

E là trung điểm của AC.

F là trung điểm của BC.

⇒ EF là đường trung bình của ΔABC. (đpcm)

b) Ta có: EF là đường trung bình của ΔABC. (cmt)

⇒ EF // AB và EF = $\frac{1}{2}$ AB.

Lại có: D là trung điểm của AB (gt) và D ∈ AB

⇒ AD  = $\frac{1}{2}$ AB và AD // EF. (2)

Từ (1), (2) ⇒ EF / AD và EF = AD.

⇒ Tứ giác AEFD là hình bình hành. (đpcm)

ΔAED có:

N là trung điểm của AE. (gt)

M là trung điểm của AD. (gt)

⇒ MN là đường trung bình của ΔAED.

⇒ MN // ED và MN = $\frac{1}{2}$  ED. (3)

Chứng minh tương tự, ta được: PQ // ED và PQ = $\frac{1}{2}$ ED.

Từ (3), (4) ⇒ MN // PQ và MN = PQ.

⇒ Tứ giác MNPQ là hình bình hành. (đpcm)

c) Khi ΔABC vuông tại A thì $\widehat{A}=90°$

Suy ra hình bình hành DAEF có $\widehat{A}=90°$  nên DAEF là hình chữ nhật

Khi đó AF = DE

Mặt khác theo tính chất đường trung bình ta có MN = $\frac{1}{2}$  DE, NP = $\frac{1}{2}$  AF

Khi đó: MN = NP

⇒ MNPQ là hình bình hành có MN = NP nên MNPQ là hình thoi.

d) ΔABC vuông tại A thì MNPQ là hình thoi.

Để tứ giác MNPQ là hình vuông thì MN vuông góc NP mà MN // DE, NP // AF (tính chất đường trung bình)

Nếu DE ⊥ AF mà DE // BC (tính chất đường trung bình). Suy ra: AF ⊥ BC

Suy ra: ΔABC vuông tại A có AF vừa là đường trung tuyến vừa là đường cao nên ΔABC vuông cân tại A.

Vậy ΔABC vuông cân tại A thì MNPQ là hình vuông.