Tìm giá trị n thuộc N thỏa mãn C 1 (n + 1) + 3C 2 (n + 2) = C 3 (n + 1)
Câu hỏi:
Tìm giá trị n ∈ ℕ thỏa mãn \(C_{n + 1}^1 + 3C_{n + 2}^2 = C_{n + 1}^3\).
Trả lời:
Điều kiện: n ≥ 2 và n ∈ ℕ
Ta có: \(C_{n + 1}^1 + 3C_{n + 2}^2 = C_{n + 1}^3\)
⇔ \(\frac{{\left( {n + 1} \right)!}}{{1!.n!}} + 3\frac{{\left( {n + 2} \right)!}}{{2!.n!}} = \frac{{\left( {n + 3} \right)!}}{{3!.\left( {n - 2} \right)!}}\)
⇔ \(n + 1 + 3.\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{2} = \frac{{\left( {n - 1} \right)n\left( {n + 1} \right)}}{6}\)
Vì n + 1 > 0 nên chia cả 2 vế cho n + 1 ta có:
⇔ 1 + \(3.\frac{{\left( {n + 2} \right)}}{2} = \frac{{\left( {n - 1} \right)n}}{6}\)
⇔ 6 + 3.3(n+2) = (n – 1)n
⇔ n2 – 10n – 24 = 0
⇔ \(\left[ \begin{array}{l}n = - 2\left( L \right)\\n = 12\end{array} \right.\)
Vậy n = 12.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong mặt phẳng cho 15 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Số tam giác có đỉnh là 3 trong số 15 điểm đã cho là?
Xem lời giải »
Câu 2:
Giải phương trình: sin2x – cos2x + 3sinx – cosx – 1 = 0.
Xem lời giải »
Câu 3:
Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.
Xem lời giải »
Câu 4:
Làm theo mẫu: \(\frac{{143}}{{10}} = 14;\frac{3}{{10}} = 0,3\).
Yêu cầu: \(\frac{{126}}{{100}} = ...;\frac{{26}}{{100}} = ...\)
\(\frac{{1246}}{{10}} = ...;\frac{6}{{10}} = ...\)
Xem lời giải »
Câu 5:
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
Xem lời giải »
Câu 6:
Cho hình thang vuông ABCD (\(\widehat A\) = \(\widehat D\)= 90°) có \[\widehat {BMC}\]= 90°, với M là trung điểm của AD. Chứng minh: AD là tiếp tuyến của đường tròn bán kính BC.
Xem lời giải »
Câu 7:
Cho hình vuông có chu vi 20cm. Nếu kéo dài mỗi cạnh của hình vuông thêm 3cm thì hình vuông mới có chu vi là bao nhiêu ?
Xem lời giải »
Câu 8:
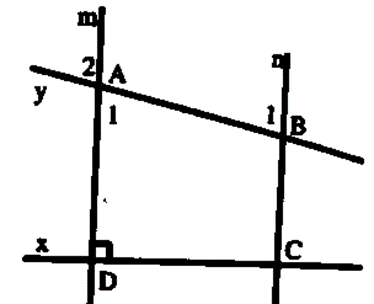
Cho hình vẽ sau, biết m // n và x ⊥ m.
1) Chứng minh: x ⊥ n.
2) Tính các góc \(\widehat {{A_1}},\widehat {{A_2}}\) biết \(\widehat {{B_1}} = 60^\circ \).
Xem lời giải »