Tìm giá trị nhỏ nhất của hàm số y = 3x + 4/x^2 trên khoảng (0; + vô cùng)
Câu hỏi:
Tìm giá trị nhỏ nhất của hàm số \(y = 3x + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
Trả lời:
Ta có: \(y' = 3 - \frac{8}{{{x^3}}}\) ⇒ \(y' = 0\) ⇔ \(3 - \frac{8}{{{x^3}}} = 0\) ⇔ \({x^3} = \frac{8}{3}\) ⇔ \(x = \frac{2}{{\sqrt[3]{3}}}\)
Hàm số y có bảng biến thiên sau:
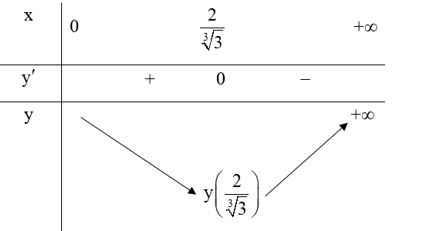
Nhìn vào bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số y trên khoảng (0; +∞) là \(y\left( {\frac{2}{{\sqrt[3]{3}}}} \right)\) ⇒ \(\mathop {\min y}\limits_{\left( {0; + \infty } \right)} = 3.\frac{2}{{\sqrt[3]{3}}} + \frac{4}{{{{\left( {\frac{2}{{\sqrt[3]{3}}}} \right)}^2}}} = 3\sqrt[3]{9}.\)
Vậy giá trị nhỏ nhất của hàm số y trên khoảng (0; +∞) là \(3\sqrt[3]{9}.\)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Xem lời giải »
Câu 2:
Gọi S là tập hợp các số tự nhiên có hai chữ số. Trong các số: 7; 15; 106; 99, số nào thuộc và số nào không thuộc tập S? Dùng kí hiệu để trả lời.
Xem lời giải »
Câu 3:
Số nghiệm của phương trình \({\log _3}x = {\log _2}\left( {1 + \sqrt x } \right)\) là
Xem lời giải »
Câu 4:
Giải phương trình: \(3{\log _3}\left( {1 + \sqrt x + \sqrt[3]{x}} \right) = 2{\log _2}\left( {\sqrt x } \right).\)
Xem lời giải »
Câu 5:
Với a là số thực dương tùy ý, tìm giá trị của log3(3a).
Xem lời giải »
Câu 6:
Một đĩa gốm cổ cần được phục hồi. Hãy xác định tâm và bán kính của đĩa. Lấy 2 điểm A, B thuộc đường tròn lớn và 2 điểm C, D thuộc đường tròn nhỏ. Xác định giao điểm 2 đường trung trực của AB và CD.
Xem lời giải »
Câu 7:
Phân tích đa thức sau thành nhân tử: x2 – 6x + 2(x – 6).
Xem lời giải »
Câu 8:
Cho hình hộp ABCD.A′B′C′D′, và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là hình gì?
Xem lời giải »



