Cho hình hộp ABCD.A′B′C′D′, và một điểm M nằm giữa hai điểm A và B. Gọi (P)
Câu hỏi:
Cho hình hộp ABCD.A′B′C′D′, và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là hình gì?
Trả lời:
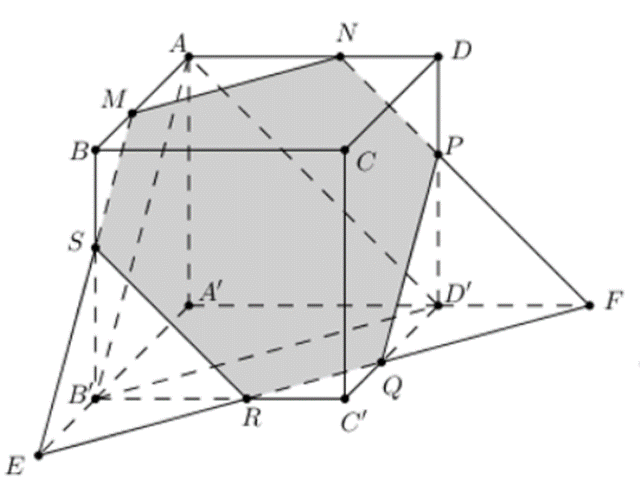
• (P) // B′D′ // BD ⊂ (ABCD)
⇒ (P) ∩ (ABCD) = MN // BD (N ∈ BC)
• (P) // AD′ ⊂ (ADD′A′)
⇒ (P) ∩ (ADD′A′) = NP // AD′ (P ∈ DD′)
• (P) // AB′ ⊂ (ABB′A′)
⇒ (P) ∩ (ABB′A′) = MS // AB′ (S ∈ BB′)
Trong mặt phẳng ABB′A′, gọi E = MS ∩ A′B′.
Trong mặt phẳng ADD′A′, gọi F = NP ∩ A′D′.
Trong mặt phẳng A′B′C′D′, ta có: EF ∩ B′C′ = R, EF ∩ C′D′ = Q.
Vậy thiết diện của hình lập phương ABCD.A′B′C′D′ khi cắt bởi mặt phẳng (P) là lục giác MNPQRS.

