Câu hỏi:
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5).
B. A(‒3; ‒1).
C. A (‒2; ‒7).
D. A(1; ‒10).
Trả lời:
Đáp án đúng là: B
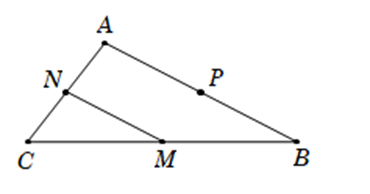
Gọi A(x; y).
Từ giả thiết, ta suy ra MN là đường trung bình của tam giác ABC nên →PA=→MN. (*)
Ta có →PA=(x+1;y−6) và →MN=(−2;−7).
Khi đó (∗)⇔{x+1=−2y−6=−7⇔{x=−3y=−1⇒A(−3;−1).
Câu 1:
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?
Câu 2:
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm (I) và (II). Mỗi sản phẩm (I) bán lãi 500 nghìn đồng, mỗi sản phẩm (II ) bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm (I) thì Chiến phải làm việc trong (3) giờ, Bình phải làm việc trong (1) giờ. Để sản xuất được một sản phẩm (II) thì Chiến phải làm việc trong (2) giờ, Bình phải làm việc trong (6) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá (180) giờ và Bình không thể làm việc quá (220) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là:
Câu 4:
Cho đường tròn (C): x2 + y2 ‒ 2x + 2y ‒ 7 = 0 và đường thẳng d: x + y + 1 = 0. Tìm tất cả các đường thẳng song song với đường thẳng d và cắt đường tròn (C) theo dây cung có độ dài bằng 2.
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(1; 2), M'(−2; −4) và số k = 2. Phép vị tự tỉ số k = 2 biến điểm M thành điểm M’ có tâm vị tự là:
Câu 7:
Cho phương trình bậc hai Az2 ‒ Bz + C . Biệt thức của phương trình được tính bởi:
Câu 8:
tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 3MC. Khi đó, biễu diễn →AM theo →AB và →AC là:
