Cho đường tròn (C): x^2 + y^2 - 2x + 2y - 7 = 0 và đường thẳng d: x + y + 1 = 0
Câu hỏi:
Cho đường tròn (C): x2 + y2 ‒ 2x + 2y ‒ 7 = 0 và đường thẳng d: x + y + 1 = 0. Tìm tất cả các đường thẳng song song với đường thẳng d và cắt đường tròn (C) theo dây cung có độ dài bằng 2.
A. x + y + 4 = 0 và x + y − 4 = 0.
B. x + y + 2 = 0.
C. x + y + 4 = 0.
D. x + y + 2 = 0 và x + y − 2 = 0.
Trả lời:
Đáp án đúng là: A
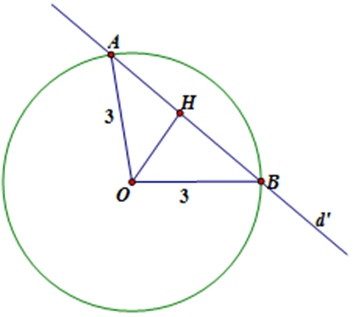
Tâm O(1; ‒1), bán kính \(R = \sqrt {{1^2} + {{( - 1)}^2} - \left( { - 7} \right)} = 3\)
Gọi đường thẳng cần tìm là d’: x + y + c = 0.
Gọi A, B lần lượt là giao điểm của d’ và (C).
Xét ∆OHB vuông tại H (H là chân đường cao kẻ từ O trong tam giác OAB ).
Ta có: \(d\left( {O,AB} \right) = \frac{{\left| {1 + \left( { - 1} \right) + c} \right|}}{{\sqrt 2 }} = OH = \sqrt {O{B^2} - B{H^2}} \)
\( = \sqrt {{3^2} - {1^2}} = 2\sqrt 2 .\)
\( \Leftrightarrow \frac{{\left| c \right|}}{{\sqrt 2 }} = 2\sqrt 2 \Leftrightarrow \left| c \right| = 4 \Leftrightarrow c = \pm 4\)
Vậy đường thẳng cần tìm có dạng x + y + 4 = 0 hoặc x + y ‒ 4 = 0.

