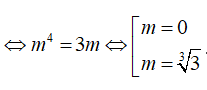Với giá trị nào của m, đồ thị hàm số y = x^4 - 2mx^2 + m^4 + 2m có ba điểm
Câu hỏi:
Với giá trị nào của m, đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều?
A. m = 0
B.
C.
D. Không tồn tại
Trả lời:
Chọn B
Hàm số có ba điểm cực trị => y’=0 có ba nghiệm phân biệt <=> m > 0.
Khi đó đồ thị hàm số có ba điểm cực trị là :
ΔABC đều khi AB = AC= BC
Ta có:
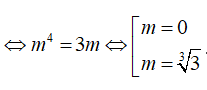
Đối chiếu với điều kiện tồn tại cực trị ta có là giá trị cần tìm.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
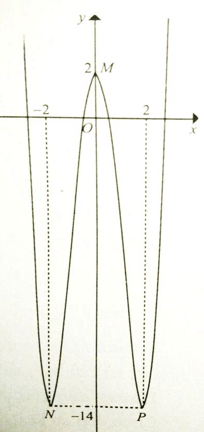
Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
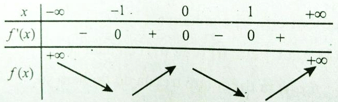
Mệnh đề nào sau đây là đúng?
Xem lời giải »
Câu 3:
Tìm a, b, c sao cho hàm số có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .
Xem lời giải »