Với giá trị nào của tham số m thì phương trình (2 + căn bậc hai 3)^x + (2 - căn bậc hai 3)

Với giá trị nào của tham số m thì phương trình \[{\left( {2 + \sqrt 3 } \right)^x} + {\left( {2 - \sqrt 3 } \right)^x} = m\] vô nghiệm.

\[{\left( {2 + \sqrt 3 } \right)^x} + {\left( {2 - \sqrt 3 } \right)^x}\] (1)

Nhận xét: \(\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right) = {2^2} - {\left( {\sqrt 3 } \right)^2} = 1 \Leftrightarrow {(2 + \sqrt 3 )^x}{(2 - \sqrt 3 )^x} = 1\)

Đặt \(t = {(2 + \sqrt 3 )^x} \Rightarrow {(2 - \sqrt 3 )^x} = \frac{1}{t},\forall t \in \left( {0; + \infty } \right)\)

pt \( \Leftrightarrow t + \frac{1}{t} = m \Leftrightarrow f\left( t \right) = t + \frac{1}{t} = m\,\,\,\,\left( 2 \right),\forall t \in \left( {0; + \infty } \right)\).

Xét hàm số \(f\left( t \right) = t + \frac{1}{t}\) xác định và liên tục trên \(\left( {0; + \infty } \right)\)

Ta có: \(f'\left( t \right) = 1 - \frac{1}{{{t^2}}} = \frac{{{t^2} - 1}}{{{t^2}}}\). Cho f’(t) = 0 khi t = 1 hoặc t = ‒1.

Bảng biến thiên:

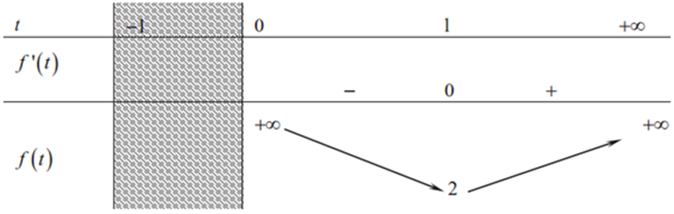
Dựa vào bảng biến thiên:

Nếu m < 2 thì phương trình (2) vô nghiệm ⇒ pt (1) vô nghiệm.