Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông
Câu hỏi:
Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
Trả lời:
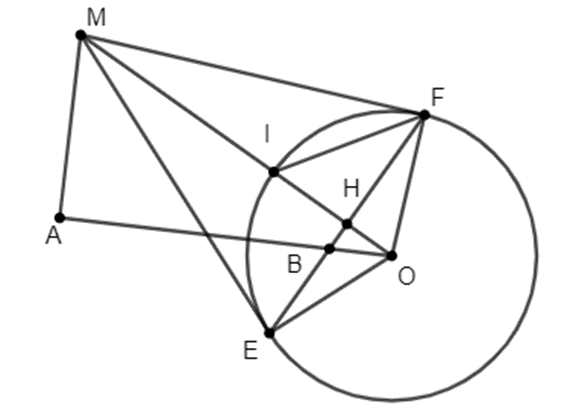
a) Do ME, MF là tiếp tuyến với đường tròn suy ra ME = MF nên M thuộc đường trung trực của EF.
Ta có OE = OF nên O thuộc đường trung trực của EF.
Do đó OM là đường trung trực của EF.
⇒ EF ⊥ OM.
Tứ giác ABHM có \(\widehat {BAM} = \widehat {BHM} = 90^\circ \), mà hai góc này ở vị trí đối nhau nên tứ giác này nội tiếp đường tròn bán kính MB.
b) Xét ∆OHB và ∆OAM có:
\(\widehat {OHB} = \widehat {OAM} = 90^\circ \); \(\widehat {MOA}\) chung
(g.g)
\( \Rightarrow \frac{{OH}}{{OA}} = \frac{{OB}}{{AM}}\)
⇒ OA.OB = OH.OM (1)
Xét ∆OHE và ∆OEM có:
\(\widehat {OHE} = \widehat {OEM} = 90^\circ \); \(\widehat {MOE}\) chung
Do đó (g.g)
Suy ra \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OM}}\)
Hay OH.OM = OE2 (2)
Từ (1) và (2) suy ra OA.OB = OH.OM = OE2 = R2.

