Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến ME
Câu hỏi:
Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến ME, MF. Biết OE = 3 cm, OM = 5 cm.
a) Tính độ dài EF.
b) Tính chu vi và diện tích tam giác MEF.
Trả lời:
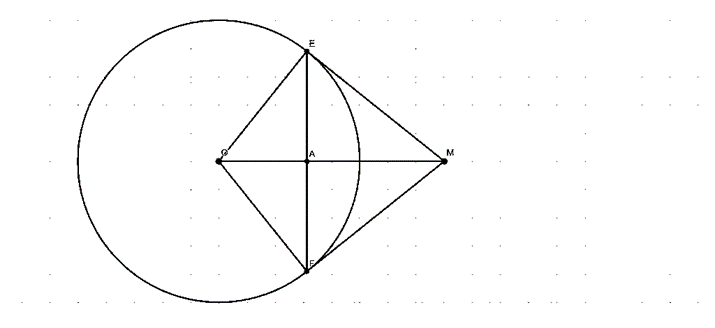
a) OM ∩ EF = {A}
OE = OF = R
ME = MF (tính chất tiếp tuyến)
Suy ra: MO là đường trung trực của EF
⇒ EA ⊥ OM; 2EA = EF
Xét ΔOEM vuông tại E có đường cao EA, có:
OE2 + ME2 = OM2
32 + ME2 = 52
ME2 = 25 – 9 = 16
ME = 4 (cm)
Lại có: \(\frac{1}{{E{A^2}}} = \frac{1}{{E{O^2}}} + \frac{1}{{E{M^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}}\)
Suy ra: EA = \(\frac{{12}}{5}\left( {cm} \right) \Rightarrow EF = 2EA = \frac{{24}}{5}\)(cm)
b) PMEF = ME + MF + EF = 2ME + EF = \(2.4 + \frac{{24}}{5} = \frac{{64}}{5}\left( {cm} \right)\)
Xét tam giác OEM vuông tại E có đường cao EA có:
EM2 = MA.MO
AM = \(\frac{{E{M^2}}}{{MO}} = \frac{{{4^2}}}{5} = \frac{{16}}{5}\)
SMEF = \(\frac{1}{2}.AM.EF = \frac{1}{2}.\frac{{16}}{5}.\frac{{24}}{5} = \frac{{192}}{{25}}\left( {c{m^2}} \right)\).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} \).
Xem lời giải »
Câu 2:
Cho biểu thức \(A = 1 + \left( {\frac{{2a + \sqrt a - 1}}{{1 - a}} - \frac{{2a\sqrt a - \sqrt a + a}}{{1 - a\sqrt a }}} \right).\frac{{a - \sqrt a }}{{2\sqrt a - 1}}\). Rút gọn A.
Xem lời giải »
Câu 4:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
Xem lời giải »
Câu 5:
Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng B qua C. Độ dài đoạn AD.
Xem lời giải »
Câu 6:
Tìm điều kiện xác định của hàm số: \(y = \frac{1}{{\sin x - \cos x}}\).
Xem lời giải »
Câu 7:
Cho \(P = \left( {\frac{1}{{\sqrt x }} + \frac{{\sqrt x }}{{\sqrt x + 1}}} \right):\frac{{\sqrt x }}{{x + \sqrt x }}\).
a) Rút gọn P.
b) Tìm giá trị của P khi x = 4.
c) Tìm x để \(P = \frac{{13}}{3}\).
Xem lời giải »
Câu 8:
Gọi x0 là nghiệm âm lớn nhất của \[\sin 9x + \sqrt 3 \cos 7x = \sin 7x + \sqrt 3 \cos 9x\]. Tìm x0?
Xem lời giải »


