Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến ME và MF
Câu hỏi:
Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến ME và MF sao cho góc EMO bằng 30 độ. Biết chu vi tam giác MEF là 30 cm. Tính:
a) Độ dài EF.
b) Diện tích tam giác MEF.
Trả lời:
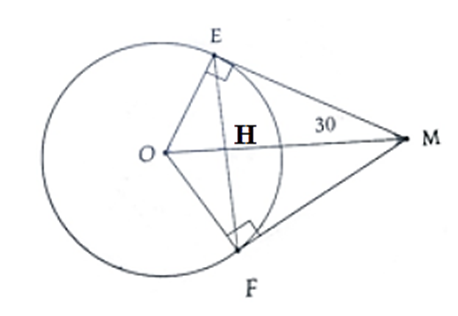
a) Ta có: ME = MF (vì ME, MF là tiếp tuyến của (O))
MO là phân giác của \(\widehat {EMF}\)
Suy ra: \(\widehat {EMF} = 2\widehat {EMO} = 2.30^\circ = 60^\circ \)
Vậy tam giác EMF đều
Suy ra: EF = EM = MF
Mà EF + EM + MF = 30
Nên: EF = EM = MF = 10(cm)
b) Gọi OM giao EF tại H
Vì EMF là tam giác đều nên MH là trung trực EF
EH = \(\frac{1}{2}EF = \frac{1}{2}.10 = 5\left( {cm} \right)\)
\(MH = \sqrt {M{E^2} - E{H^2}} = 5\sqrt 3 \)
SMEF = \(\frac{1}{2}.MH.EF = \frac{1}{2}.5\sqrt 3 .10 = 25\sqrt 3 \left( {c{m^2}} \right)\).

