Cho khối trụ có thiết diện qua trục OO′ là một hình vuông cạnh bằng 2. Mặt phẳng (P)
Câu hỏi:
Cho khối trụ có thiết diện qua trục OO′ là một hình vuông cạnh bằng 2. Mặt phẳng (P) qua trung điểm I của OO′và tạo với mặt phẳng chứa đáy góc 30°. Diện tích của thiết diện do (P) cắt khối trụ là bao nhiêu?
Trả lời:
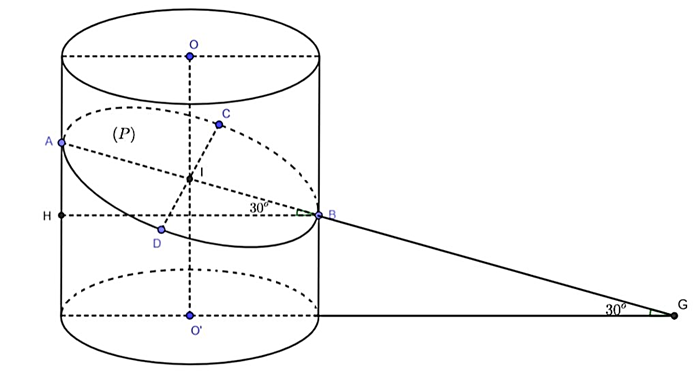
Do khối trụ có thiết diện qua trục OO′ là một hình vuông cạnh bằng 2 nên, chiều cao của khối trụ OO' = 2 và đường kính 2 mặt đáy của khối trụ bằng 2.
Giao tuyến của mặt phẳng (P) với đáy (O') là đường thẳng d.
Qua O' dựng O'G vuông góc với d
⇒ \(\widehat {\left( {\left( P \right);\left( {O'} \right)} \right)} = \left( {IG,O'G} \right) = \widehat {IGO'} = 30^\circ \)
\(\tan \widehat {IGO'} = \frac{{OI}}{{O'G}} \Rightarrow O'G = \frac{1}{{\tan 30^\circ }} = \sqrt 3 > R = 1\)
⇒ G nằm ngoài (O') suy ra thiết diện của (P) với lăng trụ là hình elip trục dài là 2a = AB, trục ngắn là 2b = CD như hình vẽ.
\(\cos \widehat {ABH} = \frac{{HB}}{{AB}} \Rightarrow AB = \frac{2}{{\cos 30^\circ }} = \frac{4}{{\sqrt 3 }}\)
⇒ \(a = \frac{2}{{\sqrt 3 }}\)
2b = CD = d = 2 ⇒ b = 1
Sthiết diện = πab = \(\frac{{2\pi }}{{\sqrt 3 }}\).

