Cho đường tròn tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO
Câu hỏi:
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a) Chứng minh MA.MB = ME.MF.
b) Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
Trả lời:
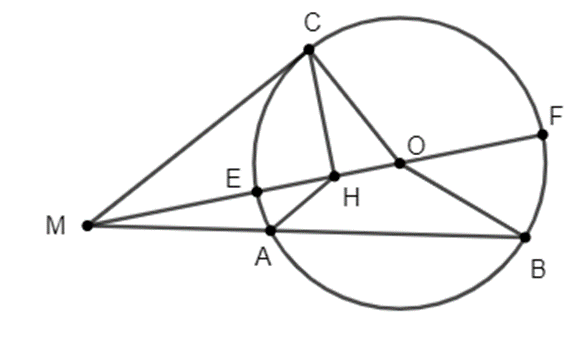
a) Hai tam giác MAE và MBF có:
\(\widehat {EMA}\) chung
\(\widehat {MAE} = \widehat {MFB}\) (cùng bù \(\widehat {EAB}\))
Do đó (g.g)
Suy ra \(\frac{{MA}}{{ME}} = \frac{{MF}}{{MB}} \Rightarrow MA.MB = ME.MF\)
b) Do hệ thức lượng trong đường tròn ta có:
MA.MB = MC2
Mặt khác, hệ thức lượng trong tam giác vuông MCO cho ta:
MH.MO = MC2 ⇒ MA.MB = MH.MO
Do đó tứ giác AHOB nội tiếp trong đường tròn.

