Cho góc xOy lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao
Câu hỏi:
Cho góc \[\widehat {xOy}\] lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao điểm của AB với tia phân giác của góc \[\widehat {xOy}\]. Chứng minh rằng: OK ^ AB.
Trả lời:
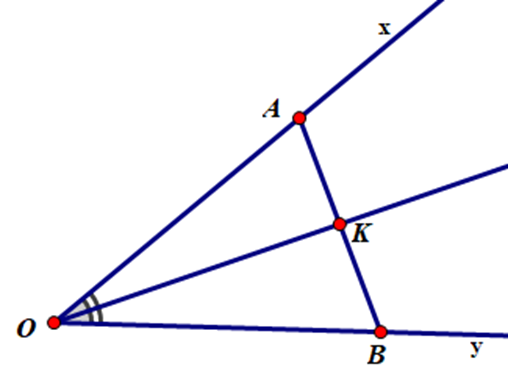
Xét ΔAKO và ΔBKO có:
OA = OB
\[\widehat {AOK} = \widehat {BOK}\] (vì OK là tia phân giác \[\widehat {xOy}\])
OK chung
Þ ΔAKO = ΔBKO (c.g.c)
\[ \Rightarrow \widehat {AKO} = \widehat {BKO}\]
Ta có: \[\widehat {AKO} + \widehat {BKO} = 180^\circ \] (vì kề bù)
\[ \Rightarrow 2\widehat {BKO} = 180^\circ \Leftrightarrow \widehat {BKO} = 90^\circ \]
Þ OK ^ AB
Vậy OK ^ AB.


