Cho hàm số y = f(x) = ax^3 + bx^2 + cx + d có đồ thị như hình bên

Câu hỏi:

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình bên. Đặt $g (x) = f (\sqrt{x^{2} + x + 2})$ . Chọn khẳng định đúng trong các khẳng định sau:

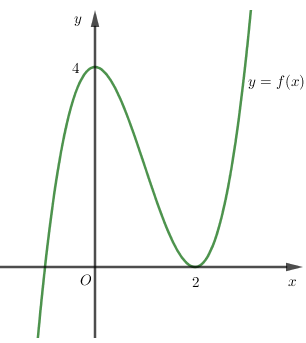
A. g(x) nghịch biến trên khoảng (0;2)

B. g(x) đồng biến trên khoảng (-1;0)

C. g(x) nghịch biến trên khoảng $(\frac{- 1}{2}; 0)$

D. g(x) đồng biến trên khoảng $(- \infty; - 1)$

Trả lời:

Đáp án C

Hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ ; $f' (x) = 3 a x^{2} + 2 b x + c$ có đồ thị như hình vẽ

Do đó $x = 0 \Rightarrow d = 4; x = 2 \Rightarrow 8 a + 4 b + 2 c + d = 0$ ; $f' (2) = 0 \Leftrightarrow 12 + 4 b + x = 0$ ; $f' (0) = 0 \Leftrightarrow c = 0$

Tìm được $a = 1; b = - 3; c = 0; d = 4$ và hàm số $y = x^{3} - 3 x^{2} + 4$

Ta có:

$g (x) = f (\sqrt{x^{2} + x + 2}) = {(\sqrt{x^{2} + x + 2})}^{3} - 3 (x^{2} + x + 2) + 4 \Rightarrow g' (x) = \frac{3}{2} (2 x + 1) \sqrt{x^{2} + x + 2} - 3 (2 x + 1) = 3 (2 x + 1) (\frac{1}{2} \sqrt{x^{2} + x + 2} - 1) g' (x) = 0 \Rightarrow [\begin{matrix} x = - \frac{1}{2} \\ x = 1 \\ x = - 2 \end{matrix}$

Bảng xét dấu của g(x):

Vậy g(x) nghịch biến trên khoảng $(\frac{- 1}{2}; 0)$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số $g_{1} (x) = 4 x + 1, g_{2} (x) = x + 2, g_{3} (x) = - 2 x + 4$ . Giá trị lớn nhất của f(x) trên R là:

Xem lời giải »

Câu 2:

Biết rằng đồ thị của hàm số $y = P (x) = x^{3} - 2 x^{2} - 5 x + 2$ cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là $x_{1}, x_{2}, x_{3}$ . Khi đó giá trị của biểu thức $T = \frac{1}{x_{1}^{2} - 4 x_{1} + 3} + \frac{1}{x_{2}^{2} - 4 x_{2} + 3} + \frac{1}{x_{3}^{2} - 4 x_{3} + 3}$ bằng:

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như sau:

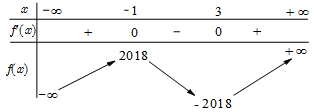
Đồ thị hàm số $y = |f (x - 2017) + 2018|$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 4:

Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.

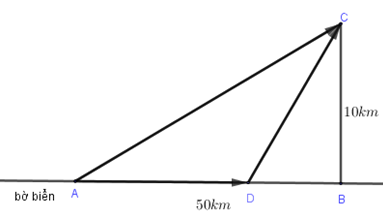
Xem lời giải »

Câu 5:

Cho hàm số y = f(x) có đạo hàm f'(x) trên R, phương trình f'(x) = 0 có 4 nghiệm thực và đồ thị hàm số f'(x) như hình vẽ. Tìm số điểm cực trị của hàm số $y = f (x^{2})$

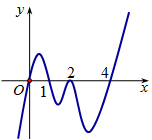
Xem lời giải »

Câu 6:

Cho đường cong $(C) : y = \frac{2 x + 3}{x - 1}$ và M là một điểm nằm trên (C). Giả sử $d_{1}, d_{2}$ tương ứng là các khoảng cách từ M đến hai tiệm cận của (C), khi đó $d_{1} . d_{2}$ bằng:

Xem lời giải »

Câu 7:

Hai điểm M, N lần lượt thuộc hai nhánh của đồ thị hàm số $y = \frac{3 x - 1}{x - 3}$ . Khi đó độ dài đoạn thẳng MN ngắn nhất bằng:

Xem lời giải »

Câu 8:

Cho hàm số $y = \frac{a x^{2} + x - 1}{4 x^{2} + b x + 9}$ có đồ thị (C), trong đó a, b là các hằng số dương thỏa mãn . Biết rằng (C) có đường tiệm cận ngang y = c và có đúng 1 đường tiệm cận đứng. Tính tổng $T = 3 a + b - 24 c$

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = f(x) = ax^3 + bx^2 + cx + d có đồ thị như hình bên

Xem thêm bài tập Toán có lời giải hay khác: