Cho hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ. Xét hàm số g(x) = f(x) - 1/3.x^3
Câu hỏi:
Cho hàm số có đồ thị như hình vẽ. Xét hàm số . Mệnh đề nào dưới đây đúng?
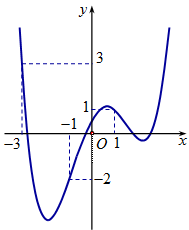
A.
B.
C.
D.
Trả lời:
Đáp án A
Ta có:
Căn cứ vào đồ thị ta có:
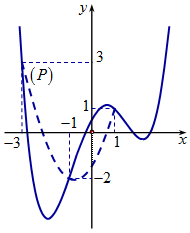
Ngoài ra, vẽ đồ thị (P) của hàm số trên cùng hệ trục tọa độ như hình vẽ bên (đường nét đứt) ta thấy (P) đi qua các điểm với đỉnh . Rõ ràng:
- Trên khoảng (-1; 1) thì , nên
- Trên khoảng (-3; -1) thì , nên
Từ những nhận định trên, ta có bảng biến thiên của hàm số trên như sau:
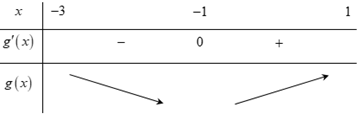
Vậy
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Điểm I(2;-3) là tâm đối xứng của những đồ thị hàm số nào dưới đây?
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên:
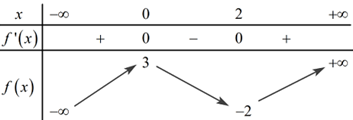
Số nghiệm của phương trình là:
Xem lời giải »
Câu 3:
Đồ thị hàm số như hình vẽ bên:
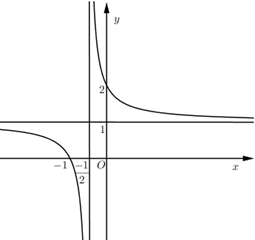
Chọn khẳng định đúng:
Xem lời giải »
Câu 4:
Cho hàm số f(x) liên tục trên và có bảng biến thiên dưới đây:
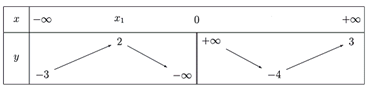
Số nghiệm của phương trình f(x) = 5 là:
Xem lời giải »
Câu 5:
Cho hàm số có đồ thị bên dưới. Khi đó giá trị m để phương trình có 3 nghiệm phân biệt, trong đó có 2 nghiệm âm và một nghiệm dương là:
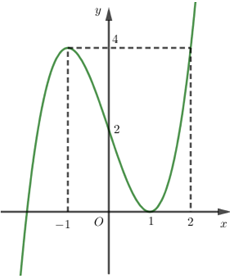
Xem lời giải »
Câu 6:
Hình vẽ bên là đồ thị hàm trùng phương. Giá trị của m để phương trình có 4 nghiệm đôi một khác nhau là:
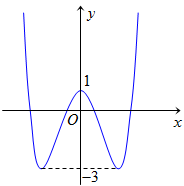
Xem lời giải »

