Cho hàm số y = f(x) liên tục trên R và có đạo hàm là f'(x) = x^2(x^2 - 4)(x^2 - 3x +2

Câu hỏi:

Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có đạo hàm là $f^{'} (x) = x^{2} (x^{2} - 4) (x^{2} - 3 x + 2) (x - 3)$ . Hàm số có bao nhiêu điểm cực đại?

A. 0

B. 2

C. 1

D. 3

Trả lời:

Đáp án C

$f^{'} (x) = x^{2} (x^{2} - 4) (x^{2} - 3 x + 2) (x - 3) = x^{2} {(x - 2)}^{2} (x + 2) (x - 1) (x - 3)$

Ta có: $f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 2 \\ x = - 2 \\ x = 1 \\ x = 3 \end{array}$

Ta có bảng xét dấu f'(x) như sau :

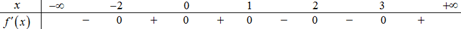
Theo bảng xét dấu trên ta suy ra hàm số có một điểm cực đại là x = 1

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Điểm cực tiểu của đồ thị hàm số $y = x^{3} - 3 x + 4$ thuộc đường thẳng nào dưới đây

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) liên tục trên $ℝ$ và có đạo hàm $f' (x) = x^{2} (x^{2} - 4) (x^{2} + 3 x + 2) (x + 3)$ . Hàm số có bao nhiêu điểm cực tiểu?

Xem lời giải »

Câu 3:

Cho hàm số f(x) có đạo hàm $f' (x) = x (x - 1) {(x + 4)}^{3}, \forall x \in ℝ$ . Số điểm cực tiểu của hàm số đã cho là

Xem lời giải »

Câu 4:

Cho hàm số f(x) có $f^{'} (x) = x^{2} (x - 1) {(x + 2)}^{5}$ . Số điểm cực trị của hàm số đã cho là

Xem lời giải »

Câu 5:

Cho hàm số $y = x^{4} - x^{2} + 1$ . Mệnh đề nào dưới đây đúng?

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = f(x) liên tục trên R và có đạo hàm là f'(x) = x^2(x^2 - 4)(x^2 - 3x +2

Xem thêm bài tập Toán có lời giải hay khác: