Cho hàm số y = f(x), y = g(x). Hai hàm số y = f'(x), y = g'(x) có đồ thị
Câu hỏi:
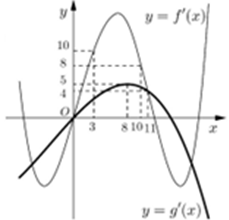
Cho hàm số . Hai hàm số có đồ thị hàm số như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số .
Hàm số đồng biến trên khoảng nào dưới đây?
A.
B.
C.
D.
Trả lời:
Đáp án B
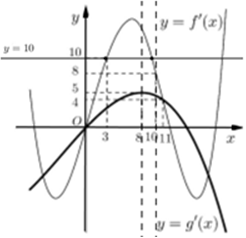
Dựa vào đồ thị hàm số ta thấy đường thẳng y = 10 cắt đồ thị hàm số y = f'(x) tại hai điểm phân biệt với mọi
Ta có:
Do đó hàm số h(x) đồng biến trên
Dựa vào các đáp án ta thấy đáp án B thỏa mãn
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số . Giá trị lớn nhất của f(x) trên R là:
Xem lời giải »
Câu 2:
Biết rằng đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là . Khi đó giá trị của biểu thức bằng:
Xem lời giải »
Câu 3:
Cho hàm số y = f(x) có bảng biến thiên như sau:
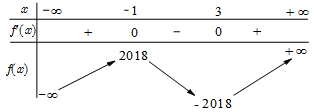
Đồ thị hàm số có bao nhiêu điểm cực trị?
Xem lời giải »
Câu 4:
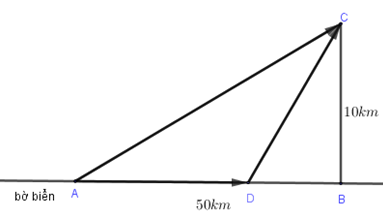
Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
Xem lời giải »
Câu 5:
Cho hàm số . Đặt (với k là số tự nhiên lớn hơn 1). Tính số nghiệm của phương trình
Xem lời giải »

