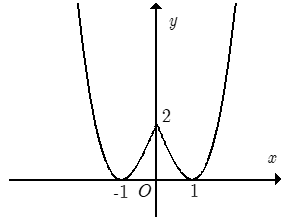
Cho hàm số y=f(x)  xác định trên  R  và có đồ thị như hình bên. Khẳng định nào sau đây là sai?

Tìm giá trị lớn nhất của hàm số  $f\left(x\right)=x^3-2x^2-4x+1$ trên đoạn  $\left[1;3\right].$

Tìm giá trị lớn nhất của hàm số  $f\left(x\right)=2x^3+3x^2-12x+2$ trên đoạn  $\left[-1;2\right].$

Biết rằng hàm số  $f\left(x\right)=x^3-3x^2-9x+28$ đạt giá trị nhỏ nhất trên đoạn [0;4] tại  $x_0$. Tính  $P=x_0+2018.$ 

Cho hàm số  $y=f\left(x\right)$ liên tục trên  $ℝ$ và có đồ thị như hình sau:

Tìm giá trị nhỏ nhất m của hàm số  $f\left(x\right)=x^2+\frac{2}{x}$ trên khoảng  $\left(0;+\infty \right).$

Gọi  $y_{\text{CT}}$ là giá trị cực tiểu của hàm số  $f\left(x\right)=x^2+\frac{2}{x}$ trên  $\left(0;+\infty \right)$. Mệnh đề nào sau đây là đúng?