Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O
Câu hỏi:
Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD lần lượt tai M, N. Chứng minh: Tứ giác BMDN là hình bình hành.
Trả lời:
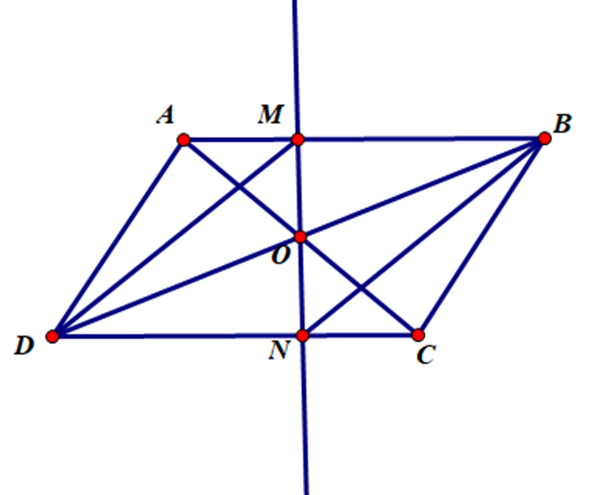
Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm mỗi đường.
Suy ra O là trung điểm của AC và BD hay OA = OC và OB = OD
Xét ΔAMO và ΔCNO có:
\[\widehat {MAO} = \widehat {NCO}\] (vì 2 góc so le trong)
OA = OC
\[\widehat {MOA} = \widehat {NOC}\] (vì 2 góc đối đỉnh)
Suy ra ΔAMO = ΔCNO (g.c.g)
Do đó OM = ON
Xét tứ giác DMBN có:
Đường chéo BD và MN cắt nhau tại O
Mà O là trung điểm của MN (do OM = ON) và O là trung điểm của BD
Suy ra DMBN là hình bình hành.
Vậy DMBN là hình bình hành.


