Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a; cạnh bên SA vuông góc với mặt đáy, SA = a căn bậc hai của 3; gọi M là trung điểm AC. Tính khoảng cách từ M đến mp(SBC).

Câu hỏi:

Trả lời:

Lời giải

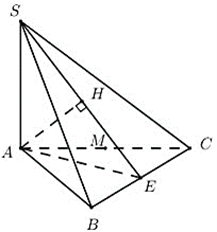
Ta có: $MA \cap \left( {SBC} \right) = C \Rightarrow \frac{{d\left( {M;\;\left( {SBC} \right)} \right)}}{{d\left( {A;\;\left( {SBC} \right)} \right)}} = \frac{{MC}}{{AC}} = \frac{1}{2}$

$\Rightarrow d\left( {M;\;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\;\left( {SBC} \right)} \right)$

Kẻ AE ^ BC; AH ^ SE ta có:

Do SA ^ (ABC) Þ SA ^ BC

Mà BC ^ AE nên suy ra BC ^ (SAE)

Þ BC ^ AH

Lại có AH ^ SE Þ AH ^ (SBC)

Þ d(A; (SBC)) = AH

Tam giác ABC đều cạnh 2a suy ra: $AE = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3$.

Xét tam giác vuông SAE, ta có:

$AH = \frac{{SA\,.\,AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \frac{{a\sqrt 3 \,.\,a\sqrt 3 }}{{\sqrt {3{a^2} + 3{a^2}} }} = \frac{{a\sqrt 6 }}{2}$

$\Rightarrow d\left( {M;\;\left( {SBC} \right)} \right) = \frac{{a\sqrt 6 }}{4}$.