Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với AB = 2a căn bậc hai 3
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với \(AB = 2a\sqrt 3 \); BC = 2a. Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60°. Khoảng cách từ D đến (SBC) tính theo a bằng
A. \(\frac{{a\sqrt {15} }}{5}\);
B. \(\frac{{2a\sqrt {15} }}{5}\);
C. \(\frac{{4a\sqrt {15} }}{5}\);
D. \(\frac{{5a\sqrt {15} }}{5}\).
Trả lời:
Đáp án đúng là: C
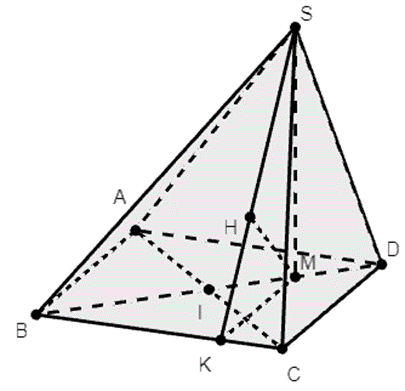
Ta có SB tạo với mp (ABCD) là: \(\widehat {SBM} = 60^\circ \)
\(BM = \frac{3}{4}BD = 3a\)
\(SM = BM.\tan 60^\circ = 3\sqrt 3 a\)
\(d\left( {D,\left( {SBC} \right)} \right) = \frac{4}{3}d\left( {M,\left( {SBC} \right)} \right) = \frac{4}{3}MH\)
Xét ∆SMK vuông tại M có:
\(\frac{1}{{M{H^2}}} = \frac{1}{{M{K^2}}} + \frac{1}{{M{S^2}}}\)
\( = \frac{1}{{{{\left( {\frac{3}{4}.2\sqrt 3 a} \right)}^2}}} + \frac{1}{{{{\left( {3\sqrt 3 a} \right)}^2}}} = \frac{5}{{27{a^2}}}\)
\( \Rightarrow MH = \sqrt {\frac{{27}}{5}} a\)
Vậy \(d\left( {D,\left( {SBC} \right)} \right) = \frac{3}{4}MH = \frac{{4\sqrt {15} a}}{5}\).

