Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật với AB = a, AD = a căn bậc hai 2
Câu hỏi:
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật với AB = a, \(AD = a\sqrt 2 \), SA = a và SA vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của AD, SC. Giả sử I là giao điểm của BM và AC. Tính thể tích tứ diện ANIB.
Trả lời:
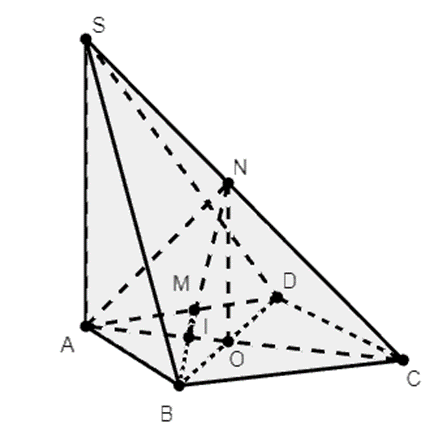
Gọi O là tâm của đáy ABCD.
Trong tam giác SAC, ta có NO là đường trung bình nên NO // SA.
Tức là NO ⊥ (ABCD) và \(NO = \frac{a}{2}\).
Ta có \({V_{ANIB}} = {V_{NAIB}} = \frac{1}{3}.{S_{AIB}}.NO = \frac{3}{6}.{S_{AIB}}(1)\)
Ta tính diện tích tam giác AIB:
Xét hình chữ nhật ABCD. Do MA = MD
\( \Rightarrow MA = \frac{1}{2}BD \Rightarrow AI = \frac{1}{2}IC\)
\( \Rightarrow AI = \frac{1}{3}AC \Rightarrow A{I^2} = \frac{{A{C^2}}}{9} = \frac{{2{a^2} + {a^2}}}{9} = \frac{{{a^2}}}{3}\)
Lại có \(BI = \frac{2}{3}BM \Rightarrow B{I^2} = \frac{4}{9}B{M^2} = \frac{4}{9}\left( {{a^2} + \frac{{{a^2}}}{2}} \right) = \frac{{2{a^2}}}{3}\)
Do đó AI2 + BI2 = a2 = AB2, nên AIB là tam giác vuông đỉnh I.
Vậy \({S_{AIB}} = \frac{1}{2}.IA.IB = \frac{1}{2}.\frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^2}\sqrt 2 }}{6}(2)\)
Thay (2) vào (1) ta có: \({V_{ANIB}} = \frac{{{a^3}\sqrt 2 }}{{36}}(dvtt)\)

