Cho tam giác đều ABC nội tiếp đường tròn tâm I đường kính AA’, M là trung điểm
Câu hỏi:
Cho tam giác đều ABC nội tiếp đường tròn tâm I đường kính AA’, M là trung điểm của BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA’ xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là V1 và V2. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
A. \(\frac{9}{4}\);
B. \(\frac{{27}}{{32}}\);
C. \(\frac{4}{9}\);
D. \(\frac{9}{{32}}\).
Trả lời:
Đáp án đúng là: D
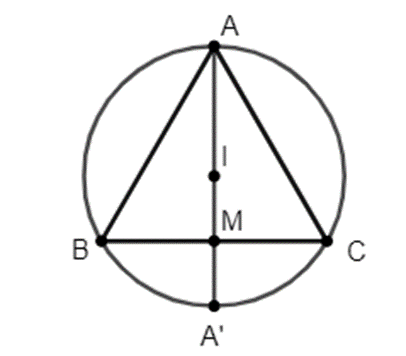
Giả sử tam giác ABC đều cạnh 1, khi đó ta có \(AM = \frac{{\sqrt 3 }}{2}\)
\( \Rightarrow AI = \frac{2}{3}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3} = R\)
\( \Rightarrow {V_2} = \frac{4}{3}\pi .{R^3} = \frac{4}{3}\pi {\left( {\frac{{\sqrt 3 }}{3}} \right)^3} = \frac{{4\sqrt 3 }}{{27}}\)
\({V_1} = \frac{1}{3}\pi .B{M^2}.AM = \frac{1}{3}\pi .{\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{{24}}\)
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{\sqrt 3 }}{{24}}}}{{\frac{{4\sqrt 3 }}{{27}}}} = \frac{9}{{32}}\)

