Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 căn bậc hai 2, cạnh bên SA
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[2\sqrt 2 \], cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Trả lời:
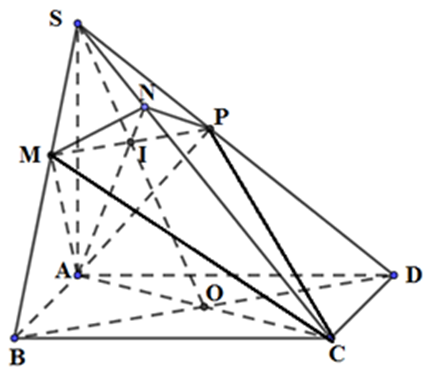
Gọi O là tâm của hình vuông ABCD ⇒O là trung điểm của AC
Ta có: CD ^ AD; CD ^ SA
Þ CD ^ (SAD)
Þ CD ^ AP
Lại có: SC ^ AP (do SC ⊥ (α)); CD ⊥ AP
⇒ AP ⊥ (SCD) ⇒ AP ⊥ CP ⇒ ΔAPC vuông tại P
⇒ OA = OC = OP
Tương tự, ta có: ΔAMC vuông tại M
⇒ OA = OC = OM
Lại có: SC ⊥ AN (do SC ⊥ (α))
⇒ΔANC vuông tại N ⇒OA = OC = ON
⇒ OA = OC = OP = OM = ON
Þ O là tâm mặt cầu ngoại tiếp tứ diện CMNP
Bán kính khối cầu là:
\[R = OA = \frac{{AB}}{{\sqrt 2 }} = 2\]
Thể tích khối cầu ngoại tiếp tứ diện CMNP là:
\[V = \frac{{4\pi }}{3} \cdot {2^3} = \frac{{32\pi }}{3}\]
Vậy thể tích khối cầu ngoại tiếp tứ diện CMNP là \[\frac{{32\pi }}{3}\].
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm giá trị lớn nhất của hàm số y = x(2 − lnx) trên đoạn [2; 3] .
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {\frac{1}{e};\,\,e} \right]\].
Xem lời giải »
Câu 3:
Tìm số giao điểm của đồ thị hàm số y = x4 − 3x2 − 5 và trục hoành.
Xem lời giải »
Câu 4:
Tìm giao điểm của đồ thị hàm số y = 2x + 1 (d) và trục hoành.
Xem lời giải »
Câu 5:
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Xem lời giải »
Câu 6:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 7:
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác ADFE là hình gì? Vì sao?
Xem lời giải »
Câu 8:
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Xem lời giải »


