Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao
Câu hỏi:
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Trả lời:
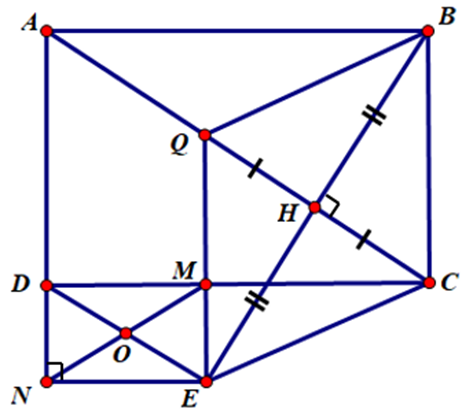
Ta có: NE ^ AD; DM ^ AD
Þ DM // NE
Xét tứ giác BCEQ có: BE ^ QC = {H}
H là trung điểm của QC
H là trung điểm của BE
Do đó BCEQ là hình thoi, suy ra BC // QE.
Mà BC // AD nên QE // AD
Xét tứ giác DMEN có: DM // NE; QE // DN
Suya ra tứ giác DMEN là hình bình hành
Mà \[\widehat {NDM} = 90^\circ \] nên tứ giác DMEN là hình chữ nhật
Do đó OM = OE
Vậy tam giác OME cân tại O.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm giá trị lớn nhất của hàm số y = x(2 − lnx) trên đoạn [2; 3] .
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {\frac{1}{e};\,\,e} \right]\].
Xem lời giải »
Câu 3:
Tìm số giao điểm của đồ thị hàm số y = x4 − 3x2 − 5 và trục hoành.
Xem lời giải »
Câu 4:
Tìm giao điểm của đồ thị hàm số y = 2x + 1 (d) và trục hoành.
Xem lời giải »
Câu 5:
Cho ΔABC vuông tại A, AB = 6 cm, AC = 8 cm. Gọi V1 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V2 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tính tỉ số \[\frac{{{V_1}}}{{{V_2}}}\].
Xem lời giải »
Câu 6:
Cho tam giác ABC, có bao nhiêu điểm M thỏa mãn: \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3?\]
Xem lời giải »
Câu 7:
Cho tích phân \[I = \mathop \smallint \limits_0^1 \frac{{{x^7}}}{{{{\left( {1 + {x^2}} \right)}^5}}}dx\], giả sử đặt t = 1 + x2. Tính tích phân I.
Xem lời giải »
Câu 8:
Cho \[\mathop \smallint \limits_0^1 \left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx = a\ln 2 + b\ln 3\]với a, b là các số nguyên. Chứng minh a + 2b = 0.
Xem lời giải »


