Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng?
Trả lời:
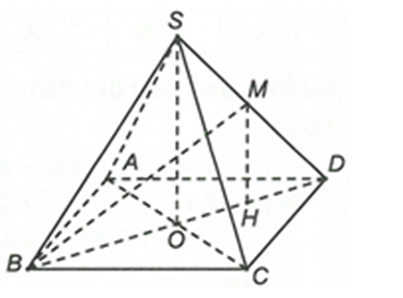
Gọi {O} = AC ∩ BD nên SO ⊥ (ABCD).
Gọi H là trung điểm của OD.
Xét ∆SOD có MH là đường trung bình nên MH // SO.
Suy ra MH ⊥ (ABCD).
Hình chiếu của đường thẳng BM trên mặt phẳng (ABCD) là BH.
Suy ra \[\widehat {\left( {BM,\left( {ABCD} \right)} \right)} = \widehat {\left( {BM,BH} \right)} = \widehat {MBH}\] là góc nhọn
Xét tam giác vuông ABD có:
\[BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = 2\sqrt 2 a.\]
\[ \Rightarrow BH = \frac{3}{4}BD = \frac{{3\sqrt 2 a}}{2}\]và \[OD = \frac{1}{2}BD = \sqrt 2 a.\]
Xét tam giác vuông SOD có:
\[SO = \sqrt {S{D^2} - O{D^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 2 a.\]
Suy ra \[MH = \frac{1}{2}SO = \frac{{\sqrt 2 a}}{2}.\]
Ta có \[\tan \widehat {MBH} = \frac{{MH}}{{BH}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{a\sqrt 2 a}}{2}}} = \frac{1}{3}\].

