Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
A. Đường thẳng qua S và song song với AD.
B. Đường thẳng qua S và song song với CD.
C. Đường SO với O là tâm hình bình hành.
D. Đường thẳng qua S và cắt AB.
Trả lời:
Đáp án đúng là: B
S là điểm chung của hai mặt phẳng (SAB) và (SCD)
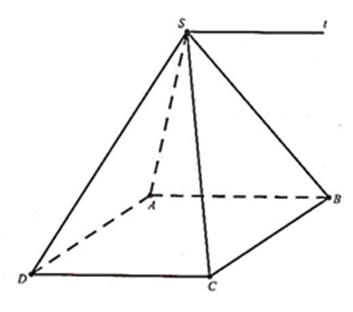
Mặt khác \[\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\CD \subset \left( {SCD} \right)\\AB//CD\end{array} \right.\]
Nên giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng St đi qua điểm S và song song với CD.

