Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc \(60^\circ .\) Tính thể tích khối chóp S.ABC.
Trả lời:
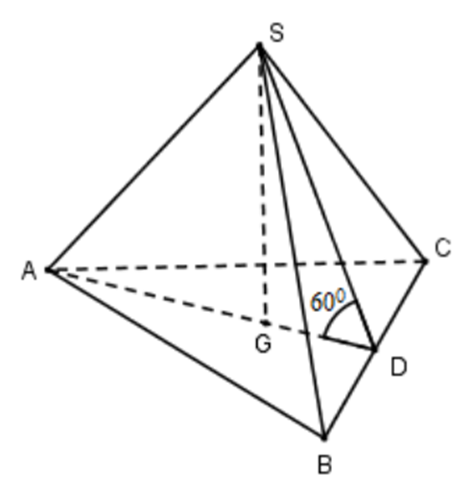
Gọi G là trọng tâm tam giác ABC. Vì chóp S.ABC đều nên SG ⊥ (ABC).
Gọi D là trung điểm của BC, ta có: AD ⊥ BC.
Ta có:
\(\left. {\begin{array}{*{20}{c}}{BC \bot AD}\\{BC \bot SG\,\,\left( {SG \bot \left( {ABC} \right)} \right)}\end{array}} \right\}\) ⇒ BC ⊥ (SAD) ⇒ BC ⊥ SD.
\(\left. {\begin{array}{*{20}{c}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{\left( {SBC} \right) \supset SD \bot BC}\\{\left( {ABC} \right) \supset AD \bot BC}\end{array}} \right\}\) ⇒ \(\left( {\widehat {\left( {SBC} \right);\left( {ABC} \right)}} \right) = \left( {\widehat {SD;AD}} \right) = \widehat {SDA} = 60^\circ \)
Vì tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\) ⇒ \(DG = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
SG ⊥ (ABC) ⇒ SG ⊥ AD ⇒ ∆SGD vuông tại G
⇒ \(SG = GD.\tan 60^\circ = \frac{{a\sqrt 3 }}{6}.\sqrt 3 = \frac{a}{2}\)
Tam giác ABC đều ⇒ \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)
⇒ \({V_{S.ABC}} = \frac{1}{3}SG.{S_{ABC}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{24}}.\)

