Cho hình chóp tứ giác đều cạnh đáy bằng a, SB = 2a. Tính thể tích khối cầu ngoại tiếp
Câu hỏi:
Cho hình chóp tứ giác đều cạnh đáy bằng a, SB = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp?
Trả lời:
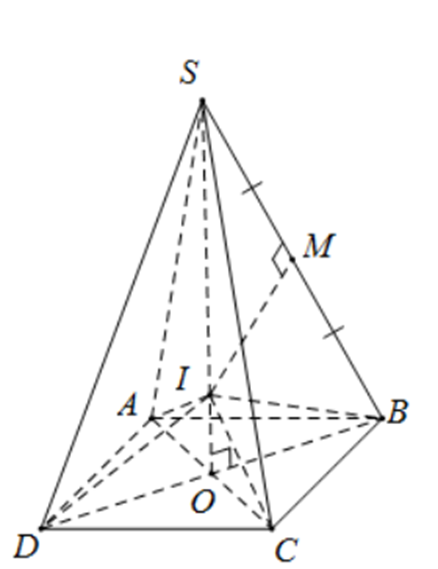
Vì S.ABCD là hình chóp đều nên đường cao SO của hình chóp cũng chính là trục của đa giác đáy
Xét ΔBCD vuông cân tại C có BC = CD = a
⇒ BD = \(\sqrt {B{C^2} + C{D^2}} = a\sqrt 2 \)
⇒ BO = \(\frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)
Xét ΔSOB vuông tại O có SB = 2a , BO = \(\frac{{a\sqrt 2 }}{2}\)
⇒ SO = \(\sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt {14} }}{2}\)
Trong mặt phẳng (SOB), ta vẽ trung trực của SB, đường này cắt SO tại I. Rõ ràng I là tâm mặt cầu ngoại tiếp S.ABCD
Gọi M là trung điểm của SB
⇒ SM = \(\frac{1}{2}SB = a\)
Xét ΔSMI và ΔSOB ta có:
Chung \(\widehat S\)
\(\widehat {SMI} = \widehat {SOB} = 90^\circ \)
⇒ ΔSMI ~ΔSOB (g.g)
⇒ \(\frac{{SI}}{{SB}} = \frac{{SM}}{{SO}}\)
⇒ SI = \(\frac{{SB.SM}}{{SO}} = \frac{{2a.a}}{{\frac{{a\sqrt {14} }}{2}}} = \frac{{2a\sqrt {14} }}{7}\)
Vì SI chính là bán kính mặt cầu ngoại tiếp S.ABCD nên ta có:
Vkhối cầu = \(\frac{4}{3}\)π.SI3 = \(\frac{{64\pi \sqrt {14} }}{{147}}\).


