Cho hình chữ nhật ABCD với AD < AB. Gọi E là điểm nằm trên đường chéo BD (0 < BE
Câu hỏi:
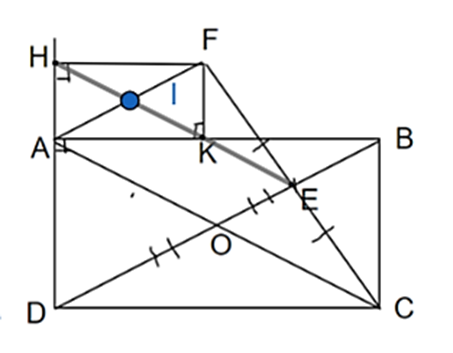
Cho hình chữ nhật ABCD với AD < AB. Gọi E là điểm nằm trên đường chéo BD (0 < BE < ED). Vẽ điểm F đối xứng với điểm C qua điểm E. Gọi H và K theo thứ tự là hình chiếu của F trên các đường thẳng AD, AB. Gọi O là giao điểm của BD, AC. Chứng minh rằng:
1) Tứ giác FHAK là hình chữ nhật.
2) FA // BD.
3) Ba điểm E, H, K thẳng hàng.
Trả lời:
a) Xét tứ giác FHAK có:
\(\widehat H = 90^\circ \)
\(\widehat {HAK} = 90^\circ \)
\(\widehat {FKA} = 90^\circ \)
⇒ Tứ giác FHAK là hình chữ nhật (đpcm)
b) Xét ΔAFC có:
FE = EC (vì F đối xứng với C qua E )
⇒ E là trung điểm của FC (1)
Vì ABCD là hình chữ nhật (gt) ⇒ O là trung điểm BD (2)
Từ (1) và (2) suy ra OE là đường trung bình của ΔAFC
⇒ OE // FA
Mà B, E, O, D thẳng hàng ⇒ BD // FA ( đpcm )
c) Gọi I là giao điểm của AF và HK
Theo tính chất hình chữ nhật thì I là trung điểm của AF
Mà E là trung điểm FC
Nên IE là đường trung bình của tam giác FAC
Suy ra: IE // AC (*)
Lại có: AF // BD nên \(\widehat {HAF} = \widehat {ADB}\)
Mà: \(\widehat {HAI} = \widehat {HAF}\)(vì AHFK là hình chữ nhật)
\(\widehat {DAB} = \widehat {ADB}\) (vì ABCD là hình chữ nhật)
Suy ra: \(\widehat {AHI} = \widehat {DAB}\) suy ra: HK // AC (**)
Từ (*) và (**) suy ra: H, K, E thẳng hàng.

