Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND. Tính
Câu hỏi:
Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND. Tính \(\widehat {BMN}\).
Trả lời:
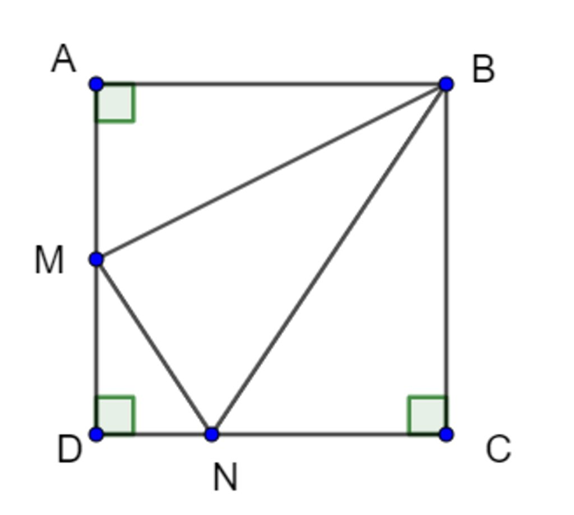
Giả sử cạnh của hình vuông ABCD là a
⇒ AB = BC = CD = AD = a
⇒ M là trung điểm của AD
⇒ AM = MD = \(\frac{a}{2}\)
NC = 2ND; NC + ND = CD
⇒ NC = \(\frac{{2a}}{3};ND = \frac{a}{3}\)
ΔABM vuông tại A có:
\(\tan \widehat {AMB} = \frac{{AB}}{{AM}} = \frac{a}{{\frac{a}{2}}} = 2\)
⇒ \[\widehat {AMB} \approx 63^\circ \]
ΔDMN vuông tại D có:
\(\tan \widehat {DMN} = \frac{{DN}}{{DM}} = \frac{{\frac{a}{3}}}{{\frac{a}{2}}} = \frac{2}{3}\)
⇒ \(\widehat {DMN} \approx 34^\circ \)
\(\widehat {AMB} + \widehat {BMN} + \widehat {DMN} = 180^\circ \)(kề bù)
⇒ \(63^\circ + \widehat {BMN} + 34^\circ = 180^\circ \)
⇒ \(\widehat {BMN} \approx 83^\circ \).

