Cho tam giác ABC vuông tại A; AB = 6; AC = 8. Phép vị tự tâm A tỷ số 3/2 đến B thành
Câu hỏi:
Cho tam giác ABC vuông tại A; AB = 6; AC = 8. Phép vị tự tâm A tỷ số \(\frac{3}{2}\) đến B thành B'; biến C thành C' tính bán kính R của đường tròn ngoại tiếp tam giác AB'C'.
Trả lời:
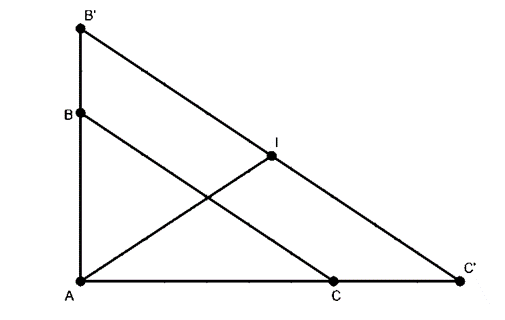
Phép vị tự tâm A tỉ số \(\frac{3}{2}\) biến B thành B' và C thành C' nên: \[\left\{ \begin{array}{l}AB' = \frac{3}{2}AB = 9\left( {cm} \right)\\AC' = \frac{3}{2}AC = 12\left( {cm} \right)\end{array} \right.\]
Gọi I là trung điểm B'C'
Do tam giác AB'C' vuông tại A nên I là tâm đường tròn ngoại tiếp tam giác AB'C'
\(B'C' = \sqrt {AB{'^2} + AC{'^2}} = \sqrt {{9^2} + {{12}^2}} = 15\left( {cm} \right)\)
\(AI = \frac{1}{2}B'C' = \frac{{15}}{2}\left( {cm} \right)\)
Vậy bán kính đường tròn ngoại tiếp tam giác AB'C' bằng \(\frac{{15}}{2}\left( {cm} \right)\).

