Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường
Câu hỏi:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
A. \(AC' = \sqrt {{a^2} + {b^2} + {c^2}} \);
B. \(AC' = \sqrt { - {a^2} + {b^2} + {c^2}} \);
C. \(AC' = \sqrt {{a^2} + {b^2} - {c^2}} \);
D. \(AC' = \sqrt {{a^2} - {b^2} + {c^2}} \).
Trả lời:
Đáp án đúng là: A
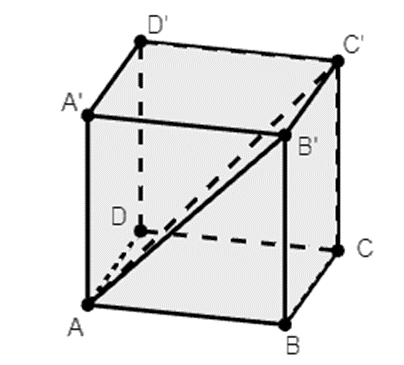
Ta có: C’B ⊥ (ABB’A’) nên suy ra ∆AB’C’ vuông tại B’.
(AB’)2 = a2 + c2
Khi đó ta có: \(AC' = \sqrt {{{(AB')}^2} + {{(B'C')}^2}} \)
\( = \sqrt {{a^2} + {c^2} + {b^2}} \).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
Xem lời giải »
Câu 2:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
Xem lời giải »
Câu 3:
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và \(\widehat {ABC} = 120^\circ \). Các cạnh AA', A'B, A'D cùng tạo với đáy một góc 60°. Tính theo a thể tích V của khối lăng trụ đã cho.
Xem lời giải »
Câu 4:
Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Xem lời giải »
Câu 5:
Chứng minh rằng với mọi số nguyên dương n ta luôn có n3 + 5n chia hết cho 6.
Xem lời giải »
Câu 6:
Cho x là số thực dương, số hạng không chứa x trong khai triển nhị thức \({\left( {x + \frac{2}{{\sqrt x }}} \right)^{30}}\) là:
Xem lời giải »
Câu 7:
Giá trị lớn nhất của hàm số y = x4 – 4x2 + 9 trên đoạn [−2; 3] bằng:
Xem lời giải »
Câu 8:
Giá trị lớn nhất của hàm số y = −x3 + 3x2 + 24x – 7 trên đoạn [−3; 3] bằng:
Xem lời giải »


