Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi
Câu hỏi:
Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa CC' và mặt phẳng (ABB'A) bằng \[\frac{{a\sqrt {12} }}{5}.\] Thể tích khối lăng trụ ABC.A'B'C bằng:
A. \(\frac{{{a^3}}}{6}.\)
B. \(\frac{{{a^3}\sqrt {21} }}{{14}}.\)
C. \(\frac{{3{a^3}}}{8}.\)
D. \(\frac{{{a^3}\sqrt {21} }}{7}.\)
Trả lời:
Đáp án đúng là: B
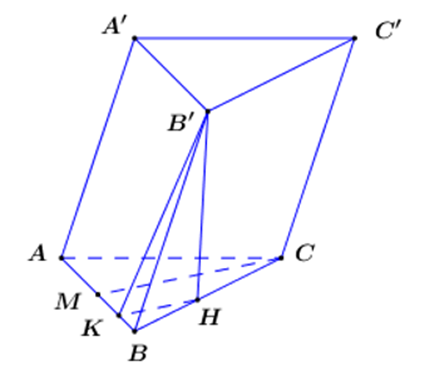
Kẻ B’H ⊥ Bc (H ∈ BC).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {BCC'B'} \right) \bot \left( {ABC} \right) = BC}\\{B'H \subset \left( {BCC'B'} \right);B'H \bot BC}\end{array} \Rightarrow B'H \bot \left( {ABC} \right)} \right.\).
Đặt \(B'H = x(x > 0)\)
\( \Rightarrow BH = \sqrt {{a^2} - {x^2}} \) (Định lí Pytago trong tam giác vuông BB’H ).
Gọi M là trung điềm của AB ta có CM ⊥ AB và \(CM = \frac{{a\sqrt 3 }}{2}\) (do ∆ABC đều ạnh \({\rm{a}}\) ).
Trong (ABC) kẻ HK // CM (K ∈ AB), áp dụng định lí Ta−lét ta có:
\(\frac{{HK}}{{CM}} = \frac{{BH}}{{BC}} \Rightarrow \frac{{HK}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt {{a^2} - {x^2}} }}{a} \Rightarrow HK = \frac{{\sqrt 3 \sqrt {{a^2} - {x^2}} }}{2}.\)
Áp dụng định lí Pytago trong tam giác vuông B’HK ta có:
\(B'{K^2} = B'{H^2} + H{K^2} = {x^2} + \frac{3}{4}\left( {{a^2} - {x^2}} \right) = \frac{3}{4}{a^2} + \frac{1}{4}{x^2} \Rightarrow B'K = \frac{{\sqrt {3{a^2} + {x^2}} }}{2}\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AB \bot B'H}\\{AB \bot HK\left( {HK\,{\rm{//}}\,CM} \right)}\end{array} \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K} \right.\).
Khi đó ta có: \({S_{ABB'A'}} = B'K.AB = \frac{{a\sqrt {3{a^2} + {x^2}} }}{2}\)
Ta có: \(CC'\,{\rm{//}}\,BB' \Rightarrow CC'\,{\rm{//}}\,\left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC';\left( {ABB'A'} \right)} \right) = d\left( {C;\left( {ABB'A'} \right)} \right) = \frac{{a\sqrt {12} }}{5}\).
\( \Rightarrow {V_{C \cdot ABB'A'}} = \frac{1}{3}{S_{ABB'A'}} \cdot d\left( {C;\left( {ABB'A'} \right)} \right)\)
\( = \frac{1}{3} \cdot \frac{{a\sqrt {3{a^2} + {x^2}} }}{2} \cdot \frac{{a\sqrt {12} }}{5}\)
\( = \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{30}} = \frac{2}{3}{V_{ABC \cdot A'B'C'}}\)
\( \Rightarrow {V_{ABC \cdot A'B'C'}} = \frac{3}{2} \cdot \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{30}} = \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{20}}\)
Lại có: \({V_{ABC \cdot A'B'C'}} = B'H \cdot {S_{\Delta ABC}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{20}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Leftrightarrow \frac{{2\sqrt {3{a^2} + {x^2}} }}{5} = x \Leftrightarrow 4\left( {3{a^2} + {x^2}} \right) = 25{x^2}\)
\( \Leftrightarrow 21{x^2} = 12{a^2} \Leftrightarrow x = \frac{{2\sqrt 7 }}{7}a\)
Vậy \({V_{ABC \cdot A'B'C'}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{2\sqrt 7 }}{7} \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{\sqrt {21} {a^3}}}{{14}}\).

