Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt đáy một
Câu hỏi:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt đáy một góc 60°. Tính thể tích của khối chóp S.ABCD ?
A. \(\frac{{{a^3}\sqrt 3 }}{2}\).
B. \(\frac{{{a^3}\sqrt 6 }}{2}\).
C. \(\frac{{{a^3}\sqrt 3 }}{6}\).
D. \(\frac{{{a^3}\sqrt 6 }}{6}\).
Trả lời:
Đáp án đúng là: D
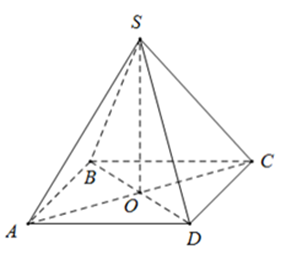
Gọi O là tâm của hình vuông ABCD ⇒ SO ⊥ (ABCD)
⇒ Góc tạo bởi cạnh bên SC và mặt đáy ABCD là \[\widehat {SCO}\], bằng 60°
\(ABCD\) là hình vuông cạnh \(a \Rightarrow \left\{ {\begin{array}{*{20}{l}}{AC = a\sqrt 2 \Rightarrow OC = \frac{a}{{\sqrt 2 }}}\\{{S_{ABCD}} = {a^2}}\end{array}} \right.\)
∆SOC vuông tại O \( \Rightarrow SO = OC \cdot {\rm{tan}}\widehat {SCO} = \frac{a}{{\sqrt 2 }} \cdot {\rm{tan}}60^\circ = \frac{{a\sqrt 3 }}{{\sqrt 2 }}\)
Thể tích khối chóp S.ABCD là: \(V = \frac{1}{3}{S_{ABCD}} \cdot SO = \frac{1}{3} \cdot {a^2} \cdot \frac{{a\sqrt 3 }}{{\sqrt 2 }} = \frac{{{a^3}\sqrt 6 }}{6}\).