Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho
Câu hỏi:
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \). Điểm M di động trên BC sao cho \(\overrightarrow {BM} = x.\overrightarrow {BC} \). Tìm x sao cho độ dài vectơ \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) đạt giá trị nhỏ nhất.
A. \(\frac{4}{5}\)
B. \(\frac{5}{6}\)
C. \(\frac{6}{5}\)
D. \(\frac{5}{4}\).
Trả lời:
Đáp án đúng là: B
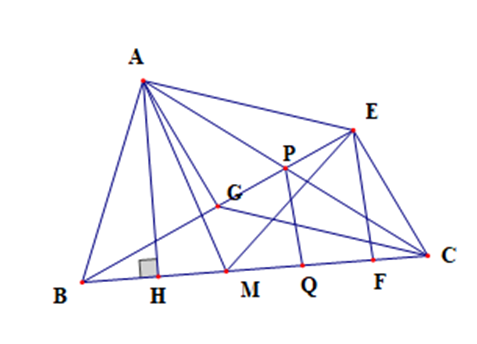
Dựng hình bình hành AGCE. Ta có
\(\overrightarrow {MA} + \overrightarrow {GC} = \overrightarrow {MA} + \overrightarrow {AE} = \overrightarrow {ME} \)
Kẻ \(EF \bot BC,F \in BC \Rightarrow |\overrightarrow {MA} + \overrightarrow {GC} | = |ME| \ge EF\)
Do đó: \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) nhỏ nhất khi M ≡ F
Gọi P là trung điểm AC, Q là hình chiếu của P trên BC
Ta có: \(BP = 3PG = \frac{3}{4}BE\)
Vì \(\left\{ \begin{array}{l}PQ \bot BC\\F{\rm{E}} \bot BC\end{array} \right. \Rightarrow PQ//F{\rm{E}}\) nên \(\widehat {BQP} = \widehat {BF{\rm{E}}}\) (hai góc đồng vị)
Xét ∆BPQ và ∆BEF có:
\(\widehat {EBF}\) là góc chung
\(\widehat {BQP} = \widehat {BF{\rm{E}}}\) (chứng minh trên)
Do đó (g.g)
\( \Rightarrow \frac{{BQ}}{{BF}} = \frac{{BP}}{{BE}} = \frac{3}{4} \Rightarrow \overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} \)
Mặt khác: \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \) nên PQ là đường trung bình của tam giác AHC
Suy ra \(\overrightarrow {HQ} = \frac{1}{2}\overrightarrow {HC} \)
Ta có:
\(\overrightarrow {BQ} = \overrightarrow {BH} + \overrightarrow {HQ} = \frac{1}{3}\overrightarrow {HC} + \frac{1}{2}\overrightarrow {HC} = \frac{5}{6}\overrightarrow {HC} = \frac{5}{8}\overrightarrow {BC} \Rightarrow \overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} = \frac{5}{6}\overrightarrow {BC} \Rightarrow x = \frac{5}{6}\)
Vậy ta chọn đáp án B.


