Cho hình thang vuông ABCD có AB = BC = a, AD = 2a. Chứng minh AC vuông góc DC
Câu hỏi:
Cho hình thang vuông ABCD có AB = BC = a, AD = 2a. Chứng minh AC vuông góc DC.
Trả lời:
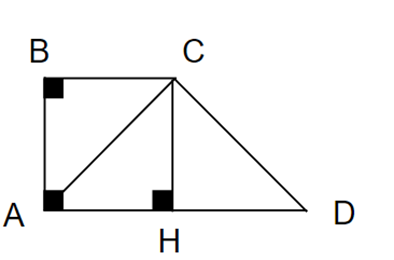
Vẽ CH vuông góc AD
Xét tứ giác ABCH có: \(\widehat A = \widehat B = \widehat H = 90^\circ \) nên ABCH là hình chữ nhật
Suy ra: AB = CH = a; BC = AH = a
Xét tam giác CHA có:
CH = HA = a
\(\widehat {CHA} = 90^\circ \)
Nên tam giác CHA vuông cân tại H
Suy ra: \(\widehat {HCA} = \widehat {AHC} = 45^\circ \)
Lại có: AD = a nên HD = AD – AH = 2a – a = a
Suy ra: CH = HD nên tam giác CHD vuông cân tại H
⇒ \(\widehat {HCD} = \widehat {CDH} = 45^\circ \)
\(\widehat {ACD} = \widehat {ACH} + \widehat {HCD} = 45^\circ + 45^\circ = 90^\circ \)
Hay AC vuông góc CD.

