Cho tam giác ABC có AB = 1, góc A = 105 độ, góc B = 60 độ. Trên cạnh BC lấy
Câu hỏi:
Cho tam giác ABC có AB = 1, \(\widehat A = 105^\circ ,\widehat B = 60^\circ \). Trên cạnh BC lấy điểm E sao cho BE = 1. Vẽ ED song song với AB. Chứng minh: \(\frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{3}\).
Trả lời:
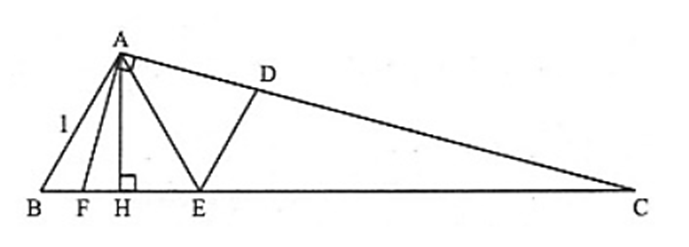
Vẽ AH ⊥ BC (H ∈ BC) ; AF ⊥ AC (F ∈ AC) (xem hình)
Từ các dữ kiện đề bài AB = BE = 1, \(\widehat {ABE} = 60^\circ \)⇒ ΔABE đều
AH ⊥ BE ⇒ AH là đường cao cũng là đường trung tuyến nên
BH = BE : 2 = 0,5
Áp dụng định lý Pi–ta–go vào ΔAHB ⊥ H:
AH2 = AB2 – BH2 = AB2 – \({\left( {\frac{{BE}}{2}} \right)^2} = 1 - \frac{1}{4} = \frac{3}{4}\left( 1 \right)\)
\(\widehat {ACB} = 180^\circ - \widehat {BAC} - \widehat {ABC} = 180^\circ - 105^\circ - 60^\circ = 15^\circ \)
\(\widehat {BAF} = \widehat {BAC} - \widehat {FAC} = 105^\circ - 90^\circ = 15^\circ \)
Suy ra: \(\widehat {ACB} = \widehat {BAF}\)
Xét tam giác ABC và tam giác FBA có:
\(\widehat {ACB} = \widehat {BAF}\)
Chung \(\widehat B\)
⇒ ∆ABC ∽ ∆FBA (g.g)
⇒ \(\frac{{AF}}{{AC}} = \frac{{AB}}{{BC}} = \frac{{BE}}{{BC}} = \frac{{AD}}{{AC}}\)(do ED // AB)
Nên AF = AD (2)
Tam giác AFC vuông tại A, đường cao AH nên có hệ thức lượng:
\(\frac{1}{{A{C^2}}} + \frac{1}{{A{F^2}}} = \frac{1}{{A{H^2}}} = \frac{4}{3}\)
Mà AF = AD nên \(\frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{3}\).

