Cho hình thang vuông ABCD, . Gọi M, N lần lượt là trung điểm của các cạnh BC, AD. Chứng minh: a) Tam giác MAD là tam giác cân.
Câu hỏi:
Cho hình thang vuông ABCD, . Gọi M, N lần lượt là trung điểm của các cạnh BC, AD. Chứng minh:
a) Tam giác MAD là tam giác cân.
Trả lời:
a)
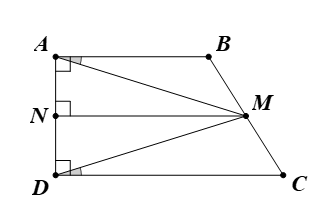
Ta có M, N lần lượt là trung điểm của BC và AD.
Suy ra MN // AB // CD.
Mà BA ⊥ AD (do ).
Do đó MN ⊥ AD.
Mà N là trung điểm của AD (giả thiết).
Vì vậy MN là đường trung trực của đoạn AD.
Suy ra MA = MD.
Vậy ∆MAD cân tại M.

